[Algorithm] Binary Search와 Parametric Search

Binary Search와 Parametric Search의 정의는 위키피디아의 Binary Search와 Parametric Serach를 참고하였습니다.

Binary Search란?

Binary Search (이진 탐색)은 들어 본 사람이 많을 것입니다. Binary Search는 정렬된 배열에서 target의 존재여부와 존재한다면 위치를 알려주는 알고리즘입니다. 여기서 중요한 것은 정렬된 배열에서만 사용할 수 있다는 것입니다. 그 이유는 Binary Search가 동작하는 방법에 담겨있습니다. 기존의 단순비교를 통한 search를 한다면 최악의 경우 배열 안에 있는 N개의 데이터 모두와 비교를 해야해서 시간복잡도가 $O(N)$인 반면에 Binary Search는 재귀적으로 탐색 범위를 반으로 줄여나가서 시간복잡도를 $O(logN)$까지 줄일 수 있는 획기적인 알고리즘입니다. 하지만 배열의 크기가 작을 때는 binary search를 사용하지 않는 것이 더 빠를때도 있습니다. 데이터의 크기와 필요에 따라 잘 사용해야겠군요!

그렇다면 탐색 범위를 재귀적으로 반으로 줄여 나간다는 것이 무슨 말일까요? Binary Search의 동작 방식을 차근차근 살펴보겠습니다.

1. 배열의 가운데 위치한 숫자와 우리가 찾는 숫자 X가 같은지 비교한다
2. 가운데 위치한 숫자와 X가 같다면 숫자가 존재한다고 반환하고 알고리즘을 끝낸다
3. 다르다면 가운데 위치한 숫자와 X를 비교한 뒤 X가 더 크다면 가운데 숫자를 기준으로 윗부분에서, X가 더 작다면 가운데 숫자를 기준으로 아랫부분에서 1~3과정을 반복한다
4. 모든 배열을 다 돌아봤는데도 숫자가 없다면 숫자가 존재하지 않는다고 반환한 뒤 알고리즘을 끝낸다

이렇게 쓰면 무슨소린지 모르겠죠? 그래서 그림도 그려봤습니다!

예제 1.

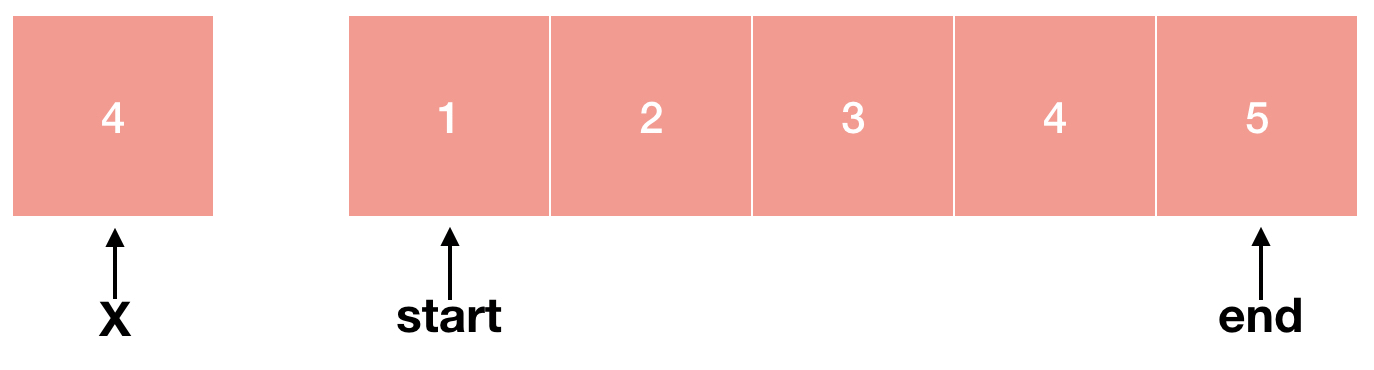
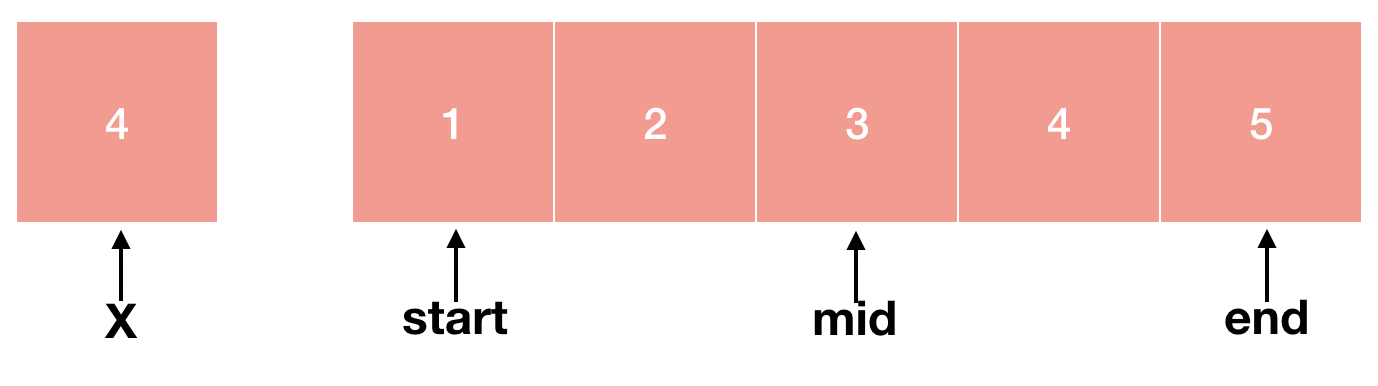
먼저 정렬된 배열과 우리가 찾으려는 숫자 X가 있습니다. 처음으로 찾고싶은 X는 4입니다.

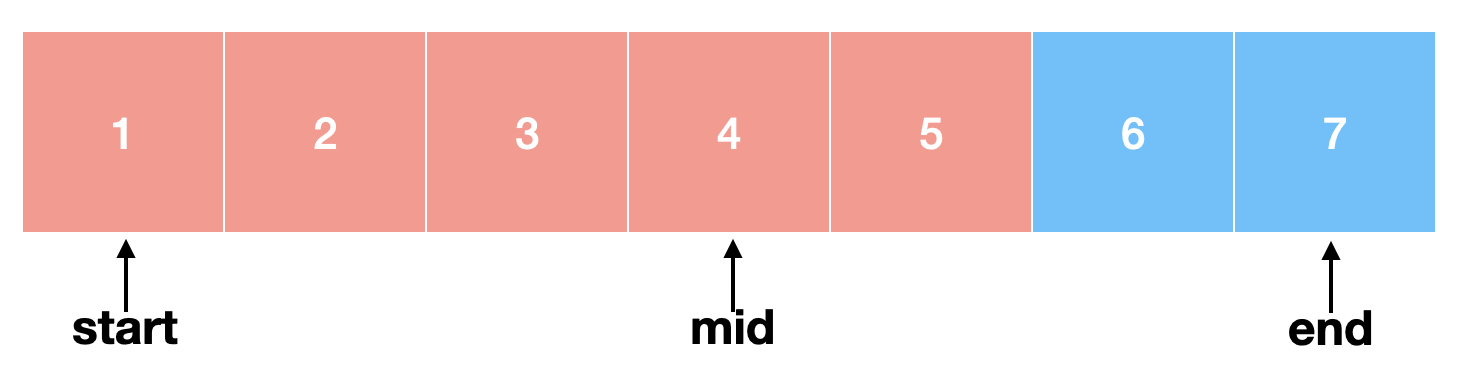
가운데 있는 숫자와 X를 비교합니다. 여기서 mid = (start + end)/2로 구할 수 있습니다. 3 < 4이기 때문에 mid보다 작은 숫자는 더 이상 비교할 필요가 없어졌습니다. 왜냐하면 정렬되어있는 배열이기 때문에 mid보다 왼쪽에 있는 숫자들은 3보다 작거나 같기 때문이죠.

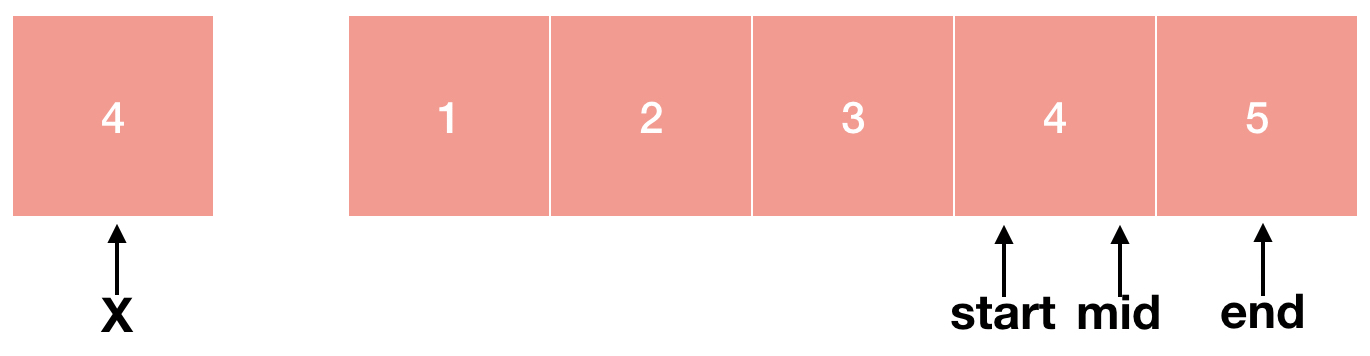
따라서 우리는 start = mid+1로 하여 탐색 범위를 mid 다음부터 end까지로 좁힐 수 있습니다. mid는 이미 우리가 찾는 숫자가 아니기 때문에 mid 다음 숫자부터 탐색을 하면 됩니다.

index는 정수이기 때문에 (start+end)/2가 나누어 떨어지지 않는 경우 소수 부분은 버리고 몫만 취하게 됩니다. 이번에는 mid에 해당하는 숫자와 X가 같기 때문에 X가 배열에 존재한다는 뜻인 1을 반환한 후 함수를 종료하게 됩니다.

예제 2.

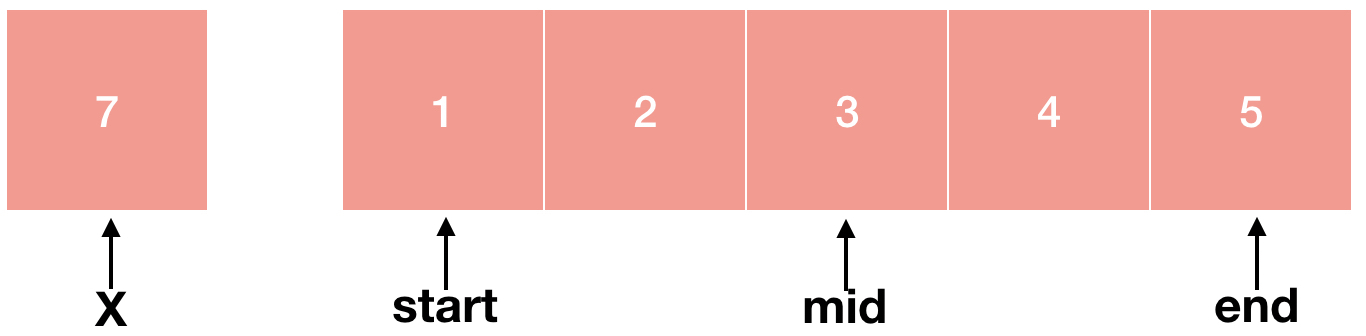
숫자가 배열 내에 존재하는 경우를 살펴봤으니 존재하지 않는 경우도 한번 살펴볼까요?

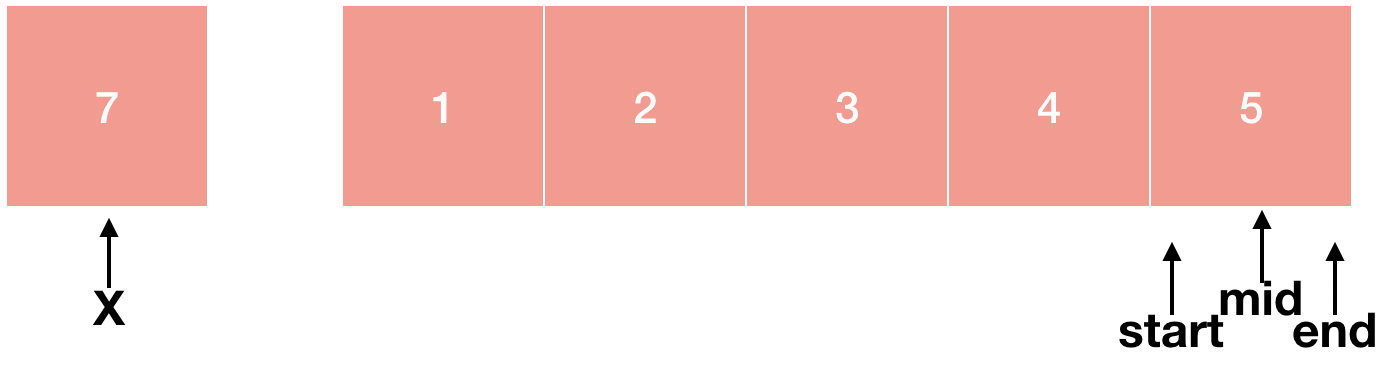
3 < 7이기 때문에 start = mid+1으로 해줍니다. 여기까지는 위와 동일합니다.

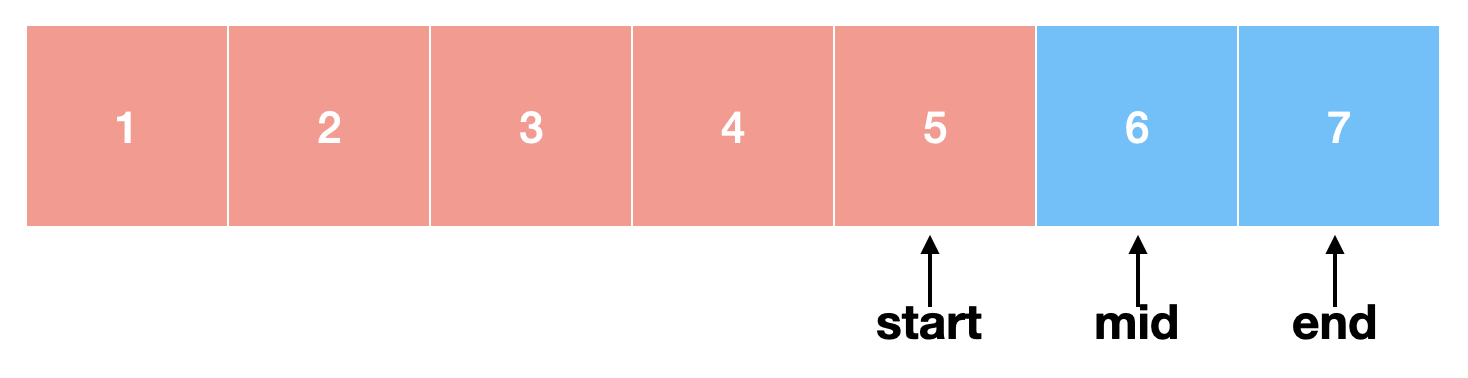
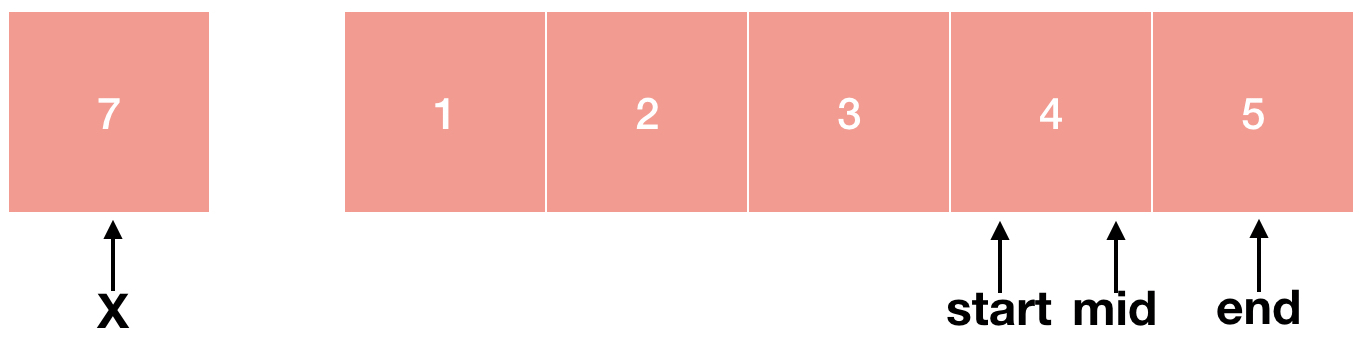
여기까지도 위와 동일합니다. index는 정수이기 때문에 start와 mid가 같아졌습니다. 하지만 4 < 7이기 때문에 start = mid+1이 됩니다.

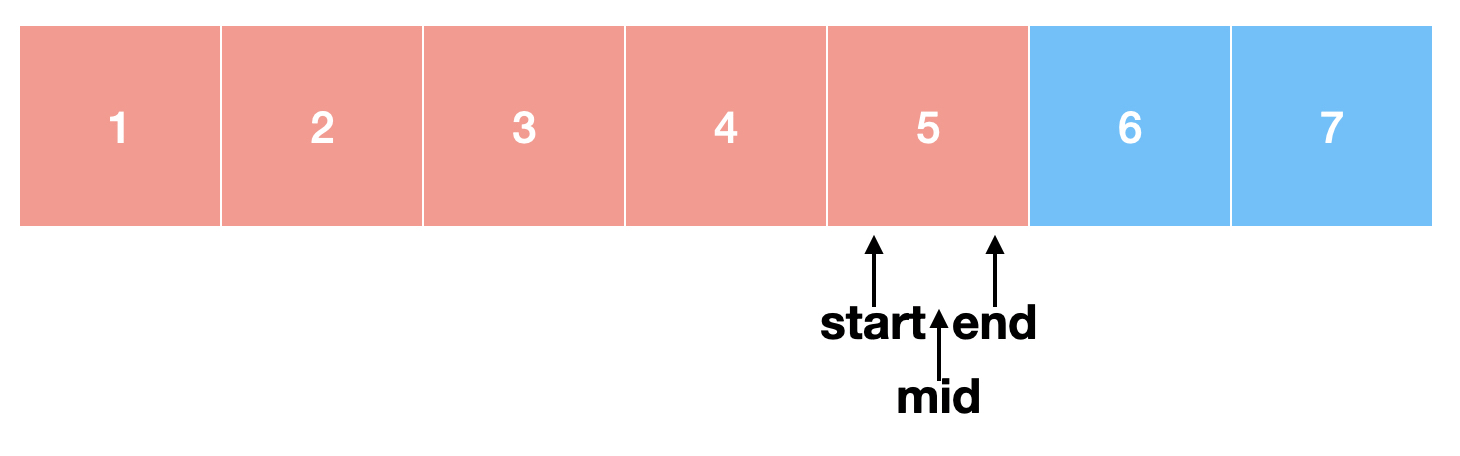
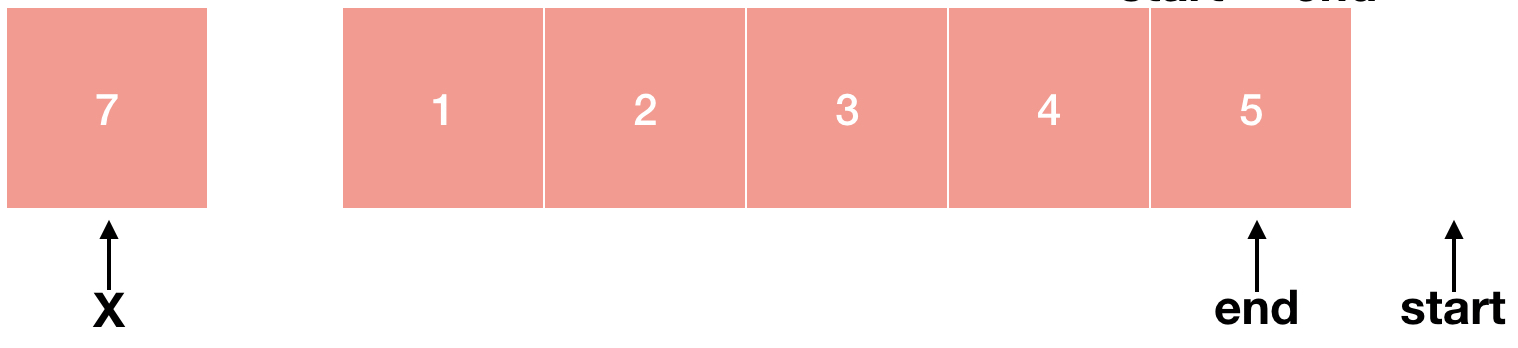
start와 mid와 end가 모두 같아졌군요. 하지만 5 < 7이기 때문에 다시 start = mid+1이 됩니다.

이런 start가 end 보다 커져버렸군요! 제가 실수한걸까요? 아닙니다! start가 end 보다 커졌다는 것은 배열을 모두 다 돌아봤는데도 우리가 찾는 숫자가 존재하지 않았다는 뜻입니다. 따라서 숫자가 존재하지 않는다는 뜻인 0을 반환하고 함수를 종료하게 됩니다.

여기까지 Binary Search에 대해 살펴봤는데요 Binary Search를 이용한 문제가 궁금하신 분은 “[백준] 1920번: 수 찾기” 포스팅을 참고하시길 바랍니다.

Parametric Search란?

Binary Search를 들어보신 분은 많은 것 같은데 Parametric Search를 들어보신 분은 상대적으로 적은 것 같습니다. 무시무시한 이름 풰뤠메트뤽 때문에 겁을 먹으시는 분들도 계신 것 같은데 전~혀 겁먹을 필요가 없습니다. 그림을 새로 그릴 필요도 없이 위에 있는 그림을 그대로 사용해도 좋을 정도로 Binary Search와 유사한 알고리즘입니다.

먼저 Parametric Search가 무엇인지 알아보도록 하겠습니다. 위키피디아에 따르면 Nimrod Megiddo라는 사람이 발명한 최적화 문제를 결정 문제로 풀 수 있는 기술이라고 하네요. 이건 또 무슨 말 일까요?

먼저 최적화 문제는 어떤 알고리즘의 최적의 솔루션을 찾아내는 것입니다. 예를 들면 오늘 기분이 좋아서 회사에 아이스크림을 5개 사갔다고 가정해봅시다. 원래 부서에는 7명이 있는데 몇명이 출장을 간다고 했던 거 같은데 기억이 안나서 대충 5개만 샀습니다. 이 때 회사에 도착했을 때 출근한 사람이 3명이라면 모두가 먹을 수 있어서 다행이겠지만 아이스크림 2개는 녹아서 버려야 될 것입니다. 하지만 출근한 사람이 7명이라면 2명은 먹을 수 없어서 삐질 수 있습니다. 이러먼 낭패겠죠. 가장 좋은 상황은 부서에 정확히 5명이 출근하는 것입니다. 이것이 바로 최적화 문제입니다. 가능한 여러개의 답 중 가장 좋은 답을 찾는 것이죠.

그렇다면 결정 문제는 무엇일까요? 결정문제는 답이 이미 결정되어있다고 보고 문제를 푸는 것 입니다. 위와 같은 상황으로 예를 들어보겠습니다. 당신은 아이스크림을 다섯개 샀는데… 이런 가게를 나오자마자 아이스크림을 몇개 샀는지 까먹어버렸어요! 이거 참… 검은 봉지에 담겨있어서 아이스크림을 몇 개 샀는지 직접 세어볼 수는 없고 부서원의 숫자를 알면 아이스크림이 모자라는지 아닌지만 알 수 있는 상황입니다. 자 머리속으로 마음대로 부서에 출근한 사람의 숫자를 정해서 시뮬레이션 해보도록 하겠습니다. 먼저 우리 부서에 3명이 출근했다고 결정해버렸습니다. 그 다음 아이스크림이 모자랄지 남을지 봉지를 만져봤더니 3개는 있는 것을 확인했습니다. 적어도 아이스크림을 못먹는 사람은 없기 때문에 부서에 3명은 출근해도 되는 상황입니다. 이번에는 부서에 7명이 출근했다고 결정해버렸습니다. 출근하지 않은 사람들한테 전화해서 출근하라고 닥달을 한거죠. 이러시면 안됩니다. 아무튼 상상이니까 했어요. 그랬더니 아이스크림이 모자라서 부서에는 7명이 출근하면 안된다는 결론이 나왔습니다. 마지막으로 부서에 5명이 출근했다고 결정했습니다. 오! 봉지를 만져보니 5명이 출근하면 모두 아이스크림을 먹을 수 있어요! 자자 여기서 멈추지 않고 당신은 6명이 출근했다고 결정을 해버립니다. 이런… 6명이 출근하면 누군가는 아이스크림을 먹을 수 없어요. 그래서 당신은 부서에는 다섯명만 출근하도록 결정했고 사실 당신은 부서장이었던거에요 최적의 솔루션을 찾았습니다.

그렇다면 Parametric Search는 언제 사용할 수 있을까요?

1. 결정문제로 풀면 쉽게 문제를 풀 수 있을 때
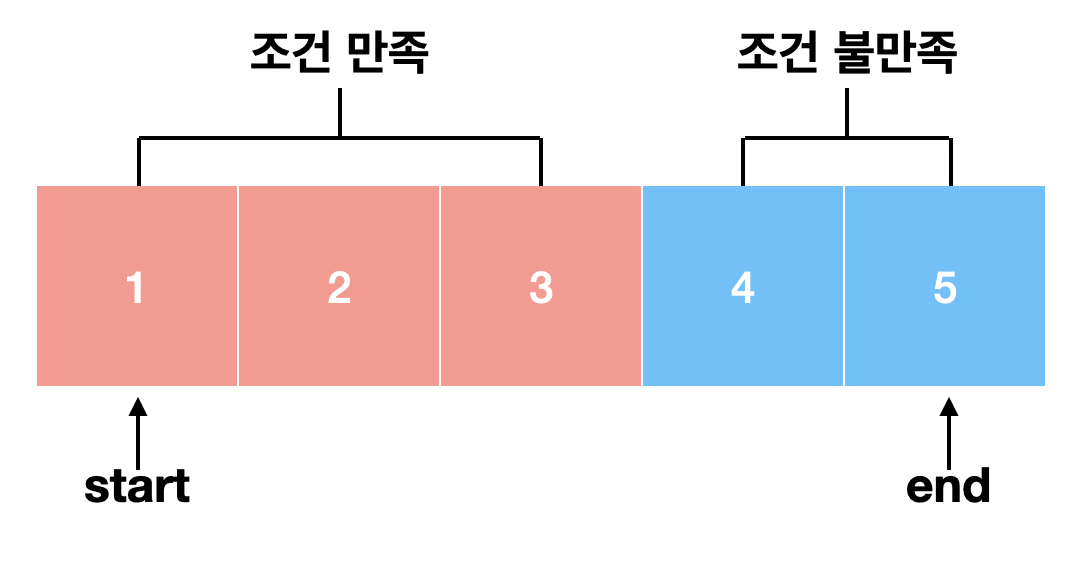
2. 어떤 시점까지는 조건을 만족하지만 그 후로는 조건을 만족하지 않는 경우 조건을 만족하는 최대값 찾기
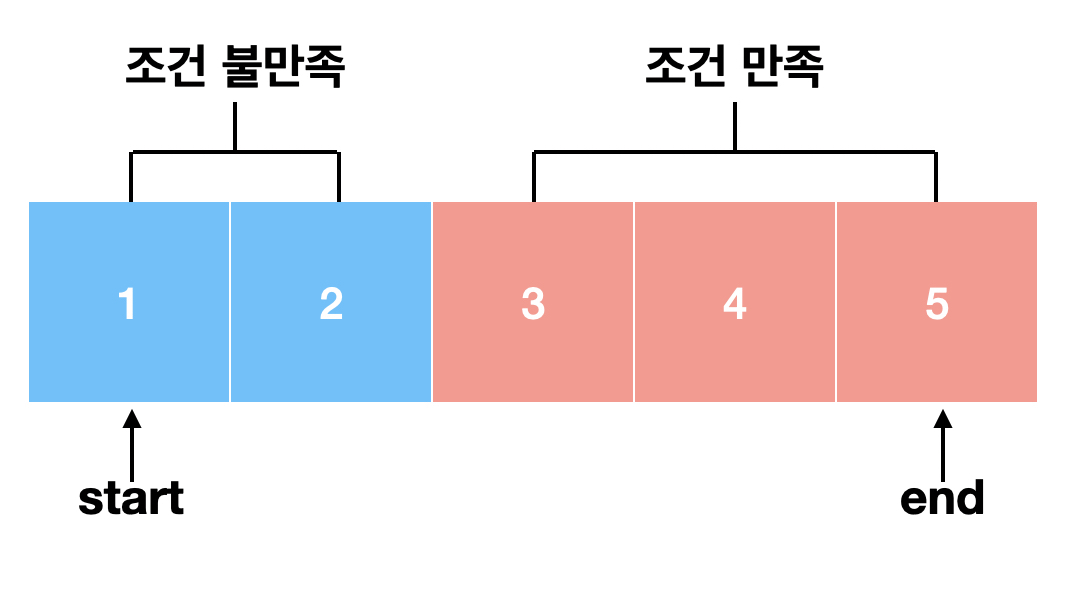
3. 반대로 어떤 시점까지는 조건을 만족하지 않지만 그 후로는 조건을 만족하는 경우 조건을 만족하는 최소값 찾기

다음으로 Parametric Search의 작동 방식에 대해 알아보겠습니다. 편의를 위해 조건을 만족하는 최대값을 찾는 문제라고 가정하고 풀어보도록 하겠습니다.

1. 배열에 가운데 위치한 숫자 X를 함수에 대입해 조건을 만족하는지 알아본다
2. 조건을 만족한다면 X보다 큰 값 중에서, 조건을 만족하지 않는다면 X보다 작은 값 중에서 1의 과정을 반복한다
3. 더 이상 살펴볼 배열이 남아있지 않는다면 알고리즘을 끝낸다

조건을 만족하는 최소값을 찾는 문제라면 2의 과정의 조건을 반대로 해주면 찾을 수 있습니다.

왜 Binary Search와 같다고 했는지 알겠죠? Binary Search와의 차이점이라면 Binary Search에서는 배열에서 X와 일치하는 값을 찾으면 바로 함수를 종료하고 위치를 반환하지만 Parametric Search는 함수를 종료하지 않고 더 이상 살펴볼 배열이 남아있지 않을때까지 탐색을 계속합니다. Binary Search와 같이 탐색 배열의 크기를 반으로 줄이면서 탐색하므로 시간복잡도는 $O(logN)$입니다.

예제

위에서 봤던 부서에 아이스크림 뿌리기를 예제로 살펴보겠습니다. 아이스크림은 총 5개이기 때문에 부서원 5명까지 출근했을 땐 모두 하나씩 먹을 수 있지만 그 이상은 아이스크림이 모자라게 됩니다.

자 이제 우리는 아이스크림이 몇 개인지 모른다고 생각해봅시다. 일단 아이스크림을 샀는데 아저씨가 검은 봉지에 담아주셔서 몇 개를 샀는지 까먹어버렸어요. 그래서 출근한 부서원의 숫자를 알면 아이스크림이 모자라는지 아닌지만 아는 상태입니다.

$(1+7)/2 = 4$이기 때문에 4명이 출근했을 때를 알아보도록 하겠습니다. 오! 4명이 출근하면 아이스크림이 모자라지 않아요! 당신은 착한 사람이기 때문에 더 많은 사람이 아이스크림을 먹을 수 있으면 좋기 때문에 탐색을 더 하기로 합니다. 따라서 start = mid+1로 하여 탐색 범위를 mid 다음부터 end까지로 좁히도록 하겠습니다. 왜냐하면 4명이 먹을 수 있다는 것은 3명 또는 2명 또는 1명이 출근해도 아이스크림을 먹을 수 있다는 것이기 때문에 더 이상 살펴볼 필요가 없습니다.

mid = 6이기 때문에 6명이 출근했을 때를 알아보도록 하겠습니다. 이런… 6명이 출근하면 누군가는 아이스크림을 먹을 수 없다고 하네요. 그렇다면 탐색범위를 다시 end=mid-1로 줄여서 살펴보도록 하겠습니다.

mid = 5이기 때문에 5명이 출근했을 때를 알아보도록 하겠습니다. 오! 5명이 출근하면 모두 아이스크림을 먹을 수 있군요. 다음 탐색을 해볼까요? 앗! start = end라서 더 이상 탐색할 부분이 남아있지 않네요! 제가 산 아이스크림은 다섯개였던게 이제야 기억이나네요!

Binary Search와 Parametric Search는 시간복잡도가 O(logN)인 만큼 데이터가 클 때 아주 유용한 알고리즘이므로 잘 알아두시면 쓸모가 많은 알고리즘입니다. 이상으로 Binary Search와 Parametric Search에 대해 알아보았습니다.