[백준] 1920번: 수 찾기

이미지를 클릭하면 문제로 이동합니다.

어떤 정수 X가 주어진 집합 안에 존재하는지 알아내는 문제입니다. 그냥 배열을 저장한 후 하나씩 대조하며 X가 존재하는지 알아내려 한다면 시간복잡도는 O(MN)만큼 걸리게 됩니다. 이렇게 하면 시간초과가 나기 때문에 시간복잡도가 O(logN)인 이진탐색(binary search)를 사용하도록 하겠습니다.

이진탐색이란 분할정복(divde and conquer)을 사용한 알고리즘으로 풀어야하는 문제의 사이즈를 줄여서 더 작은 단위의 문제를 품으로서 더 쉽고 빠르게 문제를 푸는 방법입니다.

분할정복

분할정복은 divide, conquer, combine으로 나뉘는데 이진탐색에선 divde and conquer까지만 해도 문제가 풀리게 됩니다. 분할정복은 다음과 같은 순서로 동작합니다

1. Divide: 문제를 더이상 쪼갤 수 없을 때까지 순환적으로 더 작은 단위로 쪼갠다
2. Conquer: 작아진 문제를 각각 해결한다
3. Combine: 해결된 문제들을 합쳐서 원래 문제의 답을 구한다

이진탐색

이진탐색은 정렬된 배열에서 어떤 숫자가 존재하는지 알아내는데 사용되는 알고리즘입니다. 동작 방법은 다음과 같습니다.

1. 배열의 가운데 위치한 숫자와 우리가 찾는 숫자 X가 같은지 비교한다
2. 가운데 위치한 숫자와 X가 같다면 숫자가 존재한다고 반환하고 알고리즘을 끝낸다
3. 다르다면 가운데 위치한 숫자와 X를 비교한 뒤 X가 더 크다면 가운데 숫자를 기준으로 윗부분에서, X가 더 작다면 가운데 숫자를 기준으로 아랫부분에서 1~3과정을 반복한다
4. 모든 배열을 다 돌아봤는데도 숫자가 없다면 숫자가 존재하지 않는다고 반환한 뒤 알고리즘을 끝낸다

이렇게 쓰면 무슨소린지 모르겠죠? 그래서 그림도 그려봤습니다! 예제에 있는 숫자를 사용해서 설명하도록 하겠습니다.

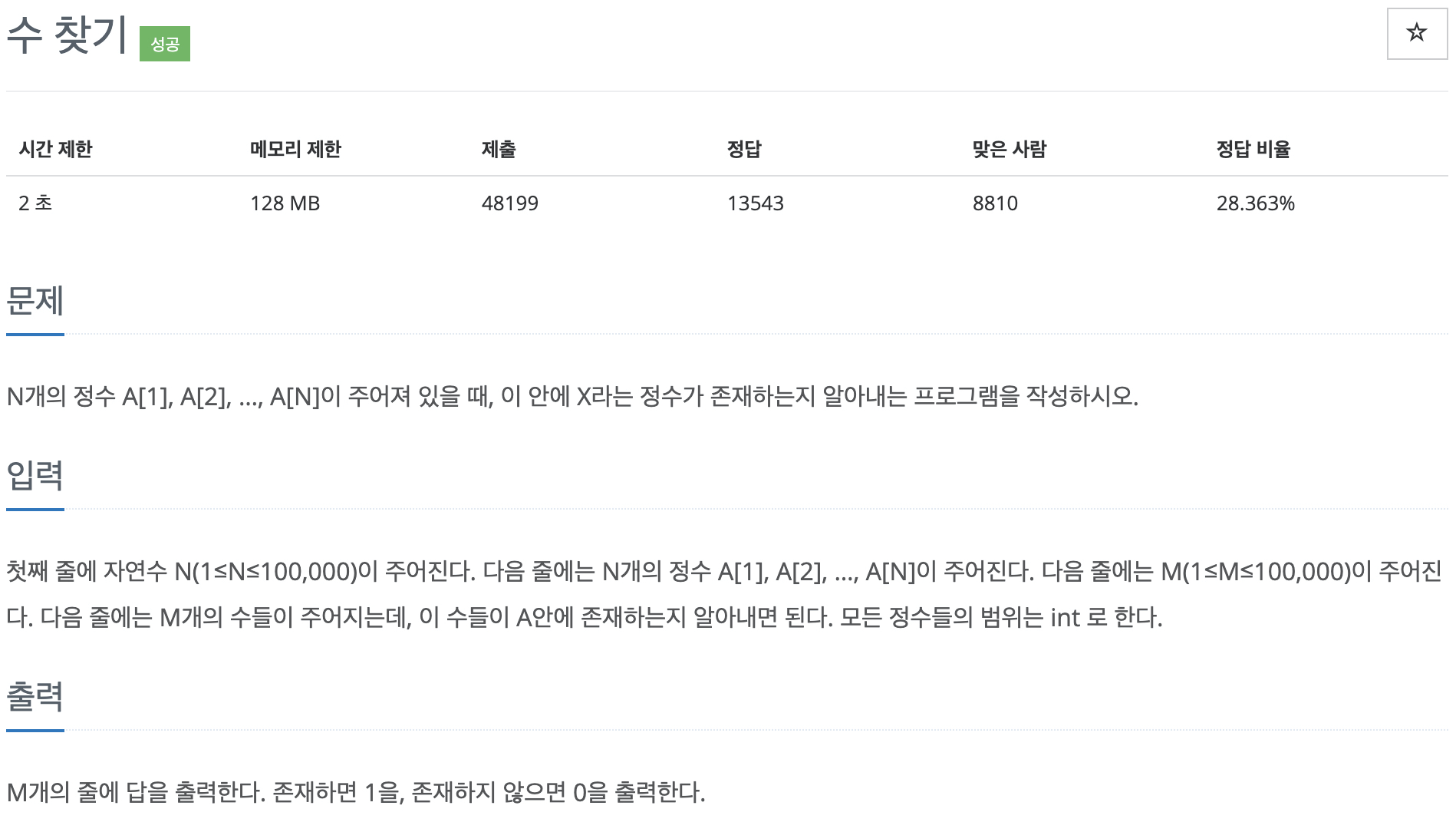
예제 1.

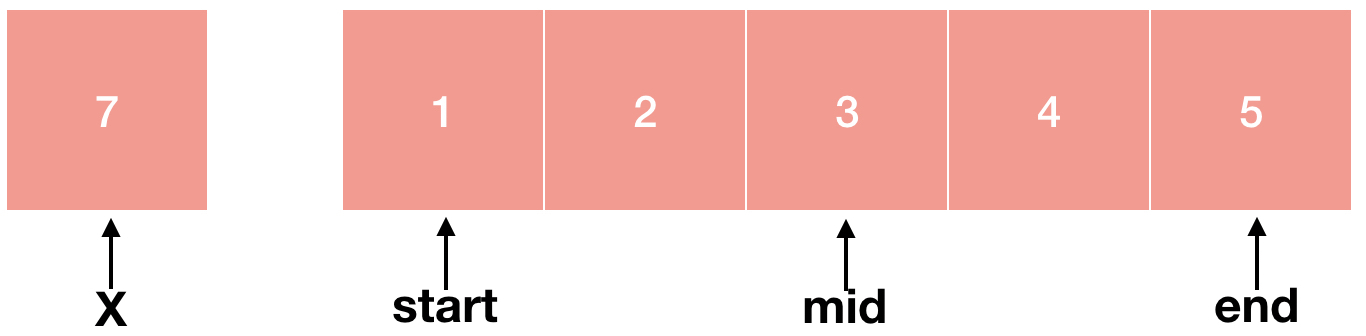
먼저 정렬된 배열과 우리가 찾으려는 숫자 X가 있습니다. 처음으로 찾고싶은 X는 4입니다.

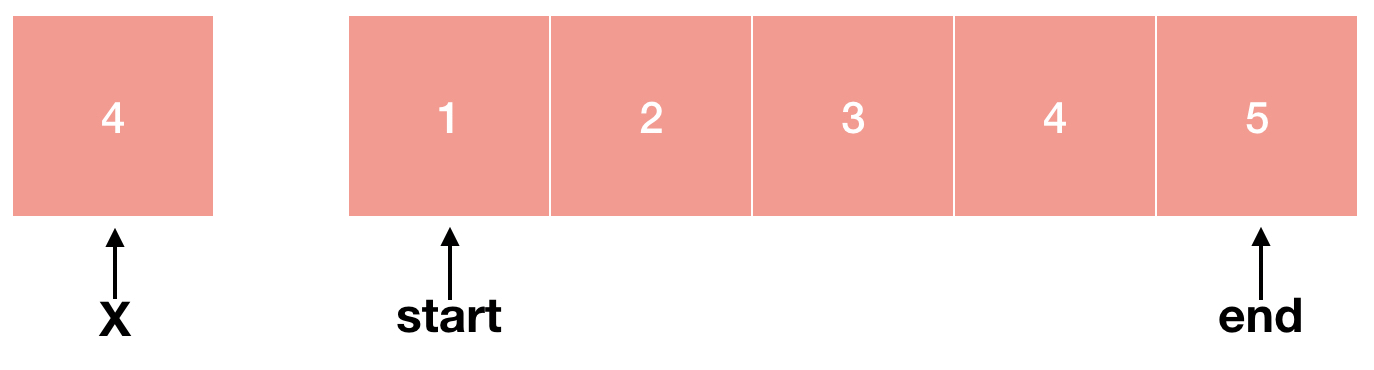
가운데 있는 숫자와 X를 비교합니다. 여기서 mid = (start + end)/2로 구할 수 있습니다. 3 < 4이기 때문에 mid보다 작은 숫자는 더 이상 비교할 필요가 없어졌습니다. 왜냐하면 정렬되어있는 배열이기 때문에 mid보다 왼쪽에 있는 숫자들은 3보다 작거나 같기 때문이죠.

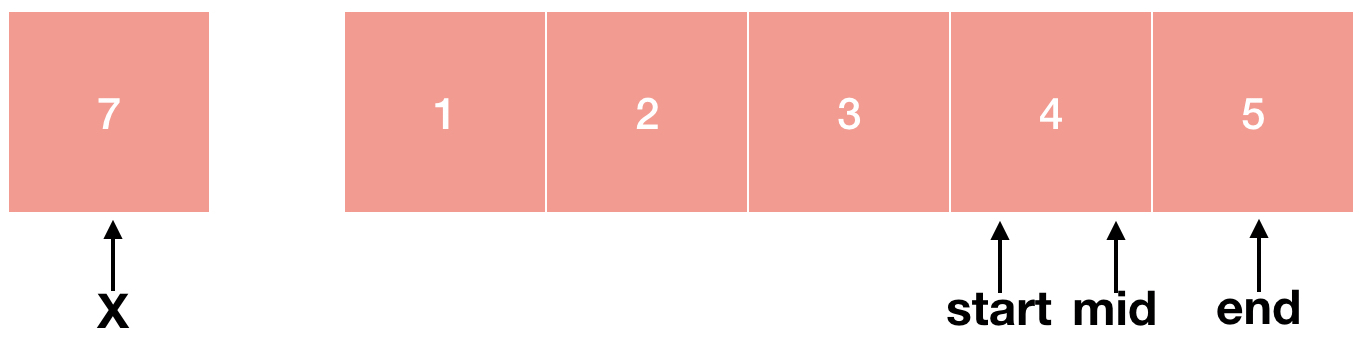
따라서 우리는 start = mid+1로 하여 탐색 범위를 mid 다음부터 end까지로 좁힐 수 있습니다. mid는 이미 우리가 찾는 숫자가 아니기 때문에 mid 다음 숫자부터 탐색을 하면 됩니다.

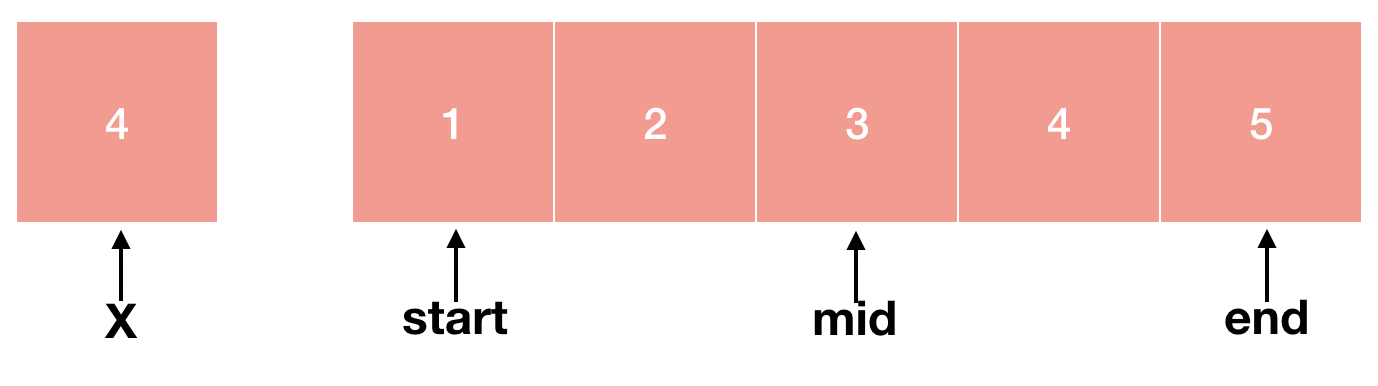
index는 정수이기 때문에 (start+end)/2가 나누어 떨어지지 않는 경우 소수 부분은 버리고 몫만 취하게 됩니다. 이번에는 mid에 해당하는 숫자와 X가 같기 때문에 X가 배열에 존재한다는 뜻인 1을 반환한 후 함수를 종료하게 됩니다.

예제 2.

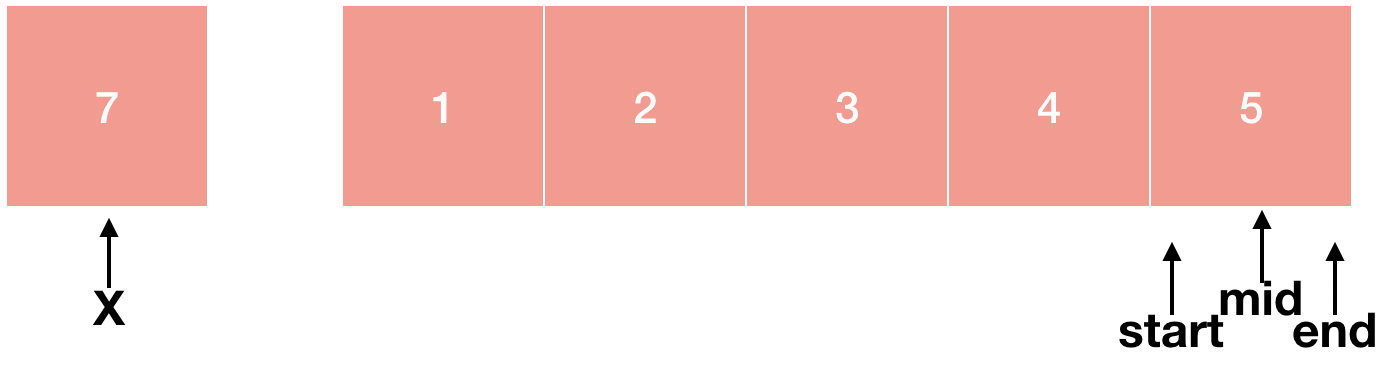
숫자가 배열 내에 존재하는 경우를 살펴봤으니 존재하지 않는 경우도 한번 살펴볼까요?

3 < 7이기 때문에 start = mid+1으로 해줍니다. 여기까지는 위와 동일합니다.

여기까지도 위와 동일합니다. index는 정수이기 때문에 start와 mid가 같아졌습니다. 하지만 4 < 7이기 때문에 start = mid+1이 됩니다.

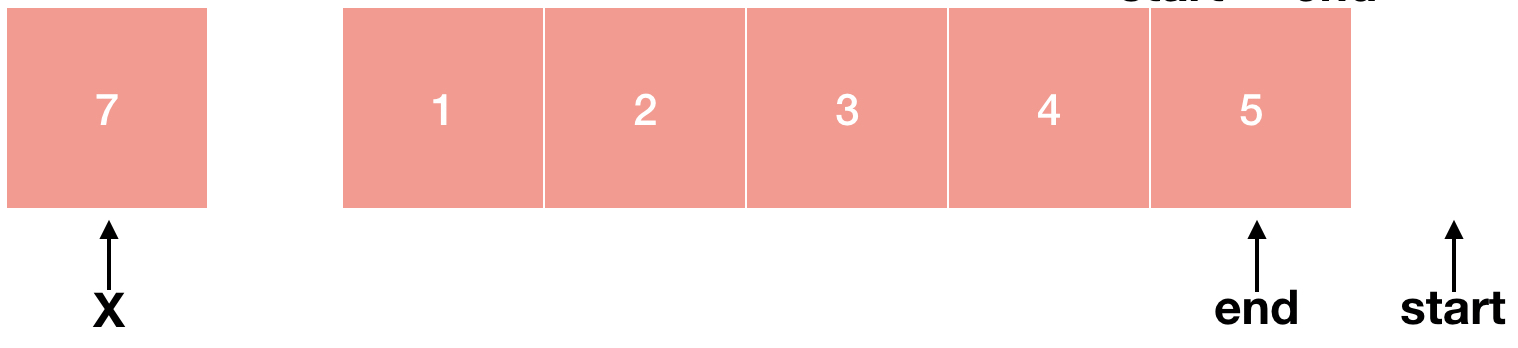
start와 mid와 end가 모두 같아졌군요. 하지만 5 < 7이기 때문에 다시 start = mid+1이 됩니다.

이런 start가 end 보다 커져버렸군요! 제가 실수한걸까요? 아닙니다! start가 end 보다 커졌다는 것은 배열을 모두 다 돌아봤는데도 우리가 찾는 숫자가 존재하지 않았다는 뜻입니다. 따라서 숫자가 존재하지 않는다는 뜻인 0을 반환하고 함수를 종료하게 됩니다.

이진탐색이 더 궁금하거나 이진탐색과 비슷한 parametric search에 대해 알고싶으신 분은 “Binary Search와 Parametric Search” 포스팅을 참고하시길 바랍니다.

Code

이진탐색을 구현하는 방법은 반복문을 사용하는 것과 재귀함수를 사용하는 것 두가지가 있습니다. 여기서는 반복문을 이용해서 구현해보도록 하겠습니다.

#include <stdio.h>
#include <algorithm>
#define MAX	100110

using namespace std;

int N, M, A[MAX], num;

void input(){
    scanf("%d", &N);
	for (int i = 1; i <= N; i++) {
		scanf("%d", &A[i]);
	}
}

bool binarySearch() {
	int s = 1, e = N, mid;
    // start > end가 되면 종료
	while (s <= e) {
		mid = (s + e) / 2;
        // mid와 우리가 찾는 숫자가 같으면 함수 종료
		if (A[mid] == num) {
			return 1;
		}
        // mid가 우리가 찾는 숫자보다 크면 mid보다 왼쪽에서 탐색
		else if (A[mid] > num) {
			e = mid - 1;
		}
        // mid가 우리가 찾는 숫자보다 작으면 mid보다 오른쪽에서 탐색
		else {
			s = mid + 1;
		}
	}
	return 0;
}


void solve(){
    input();
    sort(A+1, A+N+1);
    scanf("%d", &M);
	for (int i = 0; i < M; i++) {
		scanf("%d", &num);
		printf("%d\n", binarySearch());
	}
}


int main(void) {
    solve();
	return 0;
}