[백준] 11724번: 연결 요소의 개수

이미지를 클릭하면 문제로 이동합니다.

문제를 풀기 위해서는 먼저 연결 요소 (Connected Component)가 무엇인지 부터 알아야 합니다. 연결 요소의 정의는 위키피디아를 참고했습니다.

그래프 이론에서 연결 요소(connected component)란 무방향 그래프(undirected graph)의 부분 그래프(subgraph)로서 부분 그래프 내의 모든 정점(vertex)쌍에 대하여 항상 경로가 존재하고 다른 연결 요소와 연결되어 있지 않은 것을 말합니다. 그래프와 그래프 용어에 대한 좀 더 자세한 설명은 “[Algorithm] 그래프 기초”를 참고해주세요

연결 요소의 개수를 구하는 문제는 완전 탐색 알고리즘인 BFS와 DFS로 풀 수 있습니다. 둘 중 어느 알고리즘으로 접근해도 무방하며 하나씩 살펴보도록 하겠습니다.

1. DFS

DFS는 depth first search의 약자입니다. DFS는 아직 방문하지 않은 노드를 하나 선택하여 DFS를 한 후 이어서 해당 정점의 인접한 노드중에서 아직 방문하지 않은 노드를 선택하여 DFS를 하는 방식으로 진행됩니다. 더 이상 방문하지 않은 노드가 없다면 탐색을 종료합니다. 그림으로 살펴보도록 하겠습니다. 문제에 있는 예제 1번은 DFS와 BFS의 차이를 보기 힘들어 두번째 예제로 살펴보도록 하겠습니다.

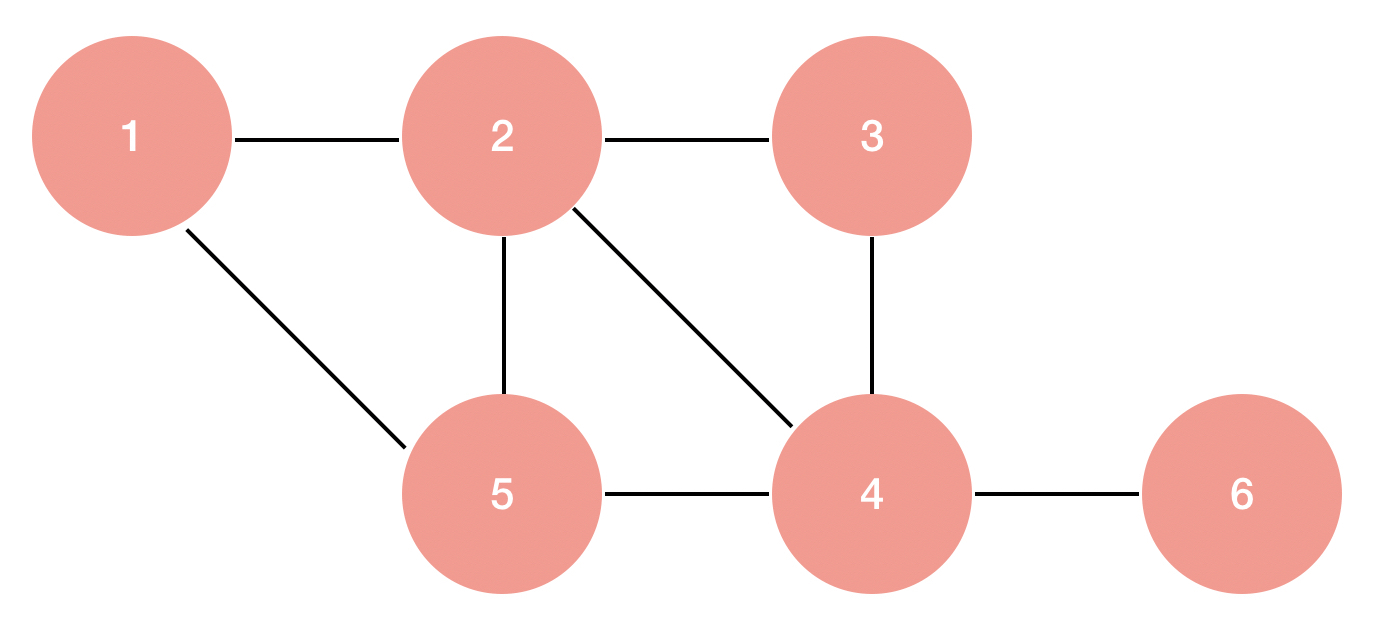
편의상 노드 1에서 탐색을 시작하고 방문할 수 있는 노드가 여러개 있는 경우 숫자가 작은 것부터 탐색한다고 가정하겠습니다.

노드 1에서 DFS를 시작하게 된다면 다음에 방문할 수 있는 노드는 노드 2 와 노드 5가 있습니다. 숫자가 작은 노드 2를 다음으로 방문합니다. 그 다음 노드 2에서부터 DFS를 다시 시행합니다. 노드 2에서는 노드 3, 노드 4, 노드 5를 방문할 수 있습니다. 가장 숫자가 작은 노드 3을 방문합니다. 같은 방식으로 노드 4를 방문 하고 노드 5를 방문합니다. 노드 5를 방문했을 때 노드 5와 인접한 노드 2와 노드 4는 이미 방문을 했기 때문에 더이상 방문할 노드가 남아있지 않습니다. 이때는 노드 5를 방문하기 전에 방문했던 노드로 되돌아가서 해당 노드에 인접한 노드 중 아직 방문하지 않은 노드가 있는지 살펴봅니다. 이 경우에선 노드 5를 방문하기 전 노드 4를 방문했기 때문에 노드 4로 돌아가 아직 방문하지 않은 노드가 있는지 살펴봅니다. 노드 4에 인접한 노드인 노드 6을 아직 방문하지 않았으므로 마지막으로 노드 6을 방문하고 탐색을 마치게 됩니다.

모든 노드를 탐색했으므로 연결요소는 1개가 있고 방문 순서는 다음와 같습니다

1 -> 2 -> 3 -> 4 -> 5 -> 6

DFS Code

#include <stdio.h>
#include <vector>
#define MAX 1010
using namespace std;

int N, M, check[MAX] = {0, }, cnt = 0;
vector <int> edges[MAX];
// 모든 간선을 저장하는 vector

void input(){
    scanf("%d %d", &N, &M);
    int a, b;
    for (int i = 0; i < M; i++){
        scanf("%d %d", &a, &b);
        // 무방향 그래프 이기 때문에 양방향으로 가는 간선을 모두 저장해주어야 합니다.
        edges[a].push_back(b);
        edges[b].push_back(a);
    }
}

void dfs(int x){
    for (int i = 0; i < edges[x].size(); i++){
        int nextNode = edges[x][i];
        if (check[nextNode] == 0){
            check[nextNode] = 1;
            dfs(nextNode);
        }
    }
}

void solve(){
    input();
    // 모든 노드를 체크하며 아직 방문 하지 않은 노드를 찾으면 conected component의 갯수를 하나 늘려주고 해당 노드로 부터 dfs를 시행합니다.
    for (int i = 1; i <= N; i++){
        if (check[i] == 0){
            check[i] = 1;
            cnt++;
            dfs(i);
        }
    }
    printf("%d\n", cnt);
}

int main(void){
    solve();
    return 0;
}

2. BFS

BFS는 breath first search의 약자입니다. BFS는 DFS와 다르게 선택된 노드에 인접만 모든 노드를 방문한 후 다음 노드로 넘어가서 탐색을 진행합니다. 같은 예제로 BFS를 시행해보도록 하겠습니다.

먼저 노드 1을 방문한 후 노드 1에 인접한 노드 2와 노드 5를 차례로 방문합니다. 더 이상 노드 1에 인접한 노드가 없으므로 이미 방문한 노드 중 하나를 선택해서 탐색을 이어갑니다. 먼저 방문한 노드 2를 선택하도록 하겠습니다. 노드 2의 인접한 노드인 노드 3과 노드 4를 차례로 방문합니다. 노드 5는 노드 2에 인접한 노드이지만 이미 방문을 했으므로 다시 방문하지 않습니다. 노드 2 다음으로 방문했던 노드 5의 인접한 노드들을 방문합니다. 하지만 노드 5에 방문한 노드인 노드 1, 노드 2, 노드 4를 이미 모두 방문했으므로 다음 노드로 넘어갑니다. 마찬가지로 다음으로 방문한 노드 3의 인접한 노드도 모두 방문했으므로 노드 4로 넘어갑니다. 노드 4의 인접한 노드 중 아직 방문하지 않은 노드 6을 방문하고 탐색을 마칩니다.

DFS와 마찬가지로 모든 노드를 방문했으므로 connected component의 개수는 1개입니다. DFS를 사용하던 BFS를 사용하던 같은 답을 얻는 것을 확인할 수 있습니다. 방문 순서는 다음과 같습니다

1 -> 2 -> 5 -> 3 -> 4-> 6

BFS Code

#include <stdio.h>
#include <vector>
#include <queue>
#define MAX 1010
using namespace std;

int N, M, check[MAX] = {0, }, cnt = 0;
vector <int> edges[MAX];
// 모든 간선을 저장하는 vector

void input(){
    scanf("%d %d", &N, &M);
    int a, b;
    for (int i = 0; i < M; i++){
        scanf("%d %d", &a, &b);
        // 무방향 그래프 이기 때문에 양방향으로 가는 간선을 모두 저장해주어야 합니다.
        edges[a].push_back(b);
        edges[b].push_back(a);
    }
}

void bfs(int x){
    queue <int> q;
    q.push(x);
    while(!q.empty()){
        int curNode = q.front();
        q.pop();
        for (int i = 0; i < edges[curNode].size(); i++){
            int nextNode = edges[curNode][i];
            if (check[nextNode] == 0){
                check[nextNode] = 1;
                q.push(nextNode);
            }
        }
    }
}

void solve(){
    input();
    // 모든 노드를 체크하며 아직 방문 하지 않은 노드를 찾으면 conected component의 갯수를 하나 늘려주고 해당 노드로 부터 bfs를 시행합니다.
    for (int i = 1; i <= N; i++){
        if (check[i] == 0){
            check[i] = 1;
            cnt++;
            bfs(i);
        }
    }
    printf("%d\n", cnt);
}

int main(void){
    solve();
    return 0;
}

DFS와 BFS에 관한 보다 기본적인 내용은 “[Algorithm] BFS DFS”를 참고해주세요!