[Algorithm] 그래프 기초

그래프의 정의는 C언어로 쉽게 풀어 쓴 자료구조 책을 참고하였습니다.

1. 그래프의 정의

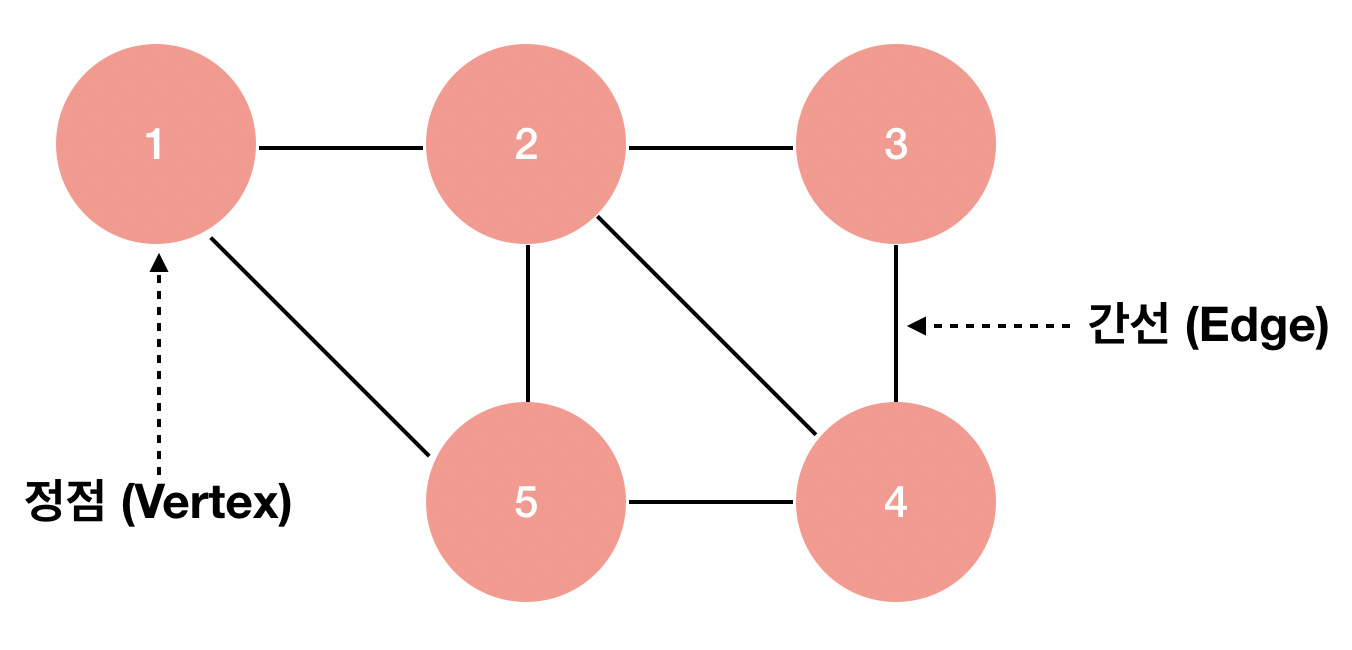
그래프는 객체 사이의 연결 관계를 표현할 수 있는 자료구조 입니다. 그래프는 정점(vertex)와 간선(edge)들의 유한집합 입니다.정점은 노드(node)라고도 불리고 간선은 링크(link)라고도 불립니다. 수학적으로는 G(V, E)로 표시하며 V(G)는 그래프 G의 정점의 집합을, E(G)는 그래프 G의 간선들의 집합을 나타냅니다.

2. 그래프 용어

무방향 그래프와 방향 그래프

간선의 종류에 따라서 그래프는 무방향 그래프(undirected graph)와 방향 그래프(directed graph)로 나뉩니다. 임의의 정점 A에서 연결된 임의의 정점 B로 가는 간선을 이용해서 거꾸로 정점 B에서 정점 A로 갈 수 있다면 무방향 그래프라고 합니다. 방향 그래프는 일방통행 길처럼 하나의 간선을 통해서는 하나의 정점만 갈 수 있는 그래프를 말합니다. 보통 무방향 그래프의 간선은 선으로, 방향 그래프의 간선은 화살표로 표현합니다.

네트워크

간선에 가중치를 할당하게 되면 두 정점간의 연결 유무뿐만 아니라 연결 강도까지 나타낼 수 있습니다. 간선에 비용이나 가중치가 할당 된 그래프를 가중치 그래프(weighted graph) 또는 네트워크(network)라고 합니다.

추후에 가중치 그래프를 이용해서 출발점에서 목적지까지 가는 가장 빠른 경로를 찾는 문제 등에 사용하게 됩니다.

부분 그래프

어떤 그래프의 정점의 일부와 간선의 일부로 이루어진 그래프를 부분 그래프(subgraph)라고 합니다. 그래프 G의 부분 그래프 S는 다음과 같은 수식을 만족시키는 그래프입니다.

\[V(S) \subseteq V(G) \\ E(S) \subseteq E(G)\]

정점의 차수

그래프에서 인접 정점(adjacent vertex)란 간선에 의해 직접 연결된 정점을 뜻합니다. 무방향 그래프에서 정점의 차수란 그 정점에 인접한 정점의 수를 말합니다.

무방향 그래프에서 모든 정점의 차수를 합하면 간선 수의 2배가 됩니다. 왜냐하면 하나의 간선은 두개의 정점에 인접하기 때문입니다. 방향 그래프에서는 오부에서 오는 간선의 개수를 진입 차수(in-degree)라고 하고 외부로 향하는 간선의 개수를 진출 차수(out-degree)라고 합니다.

연결 그래프

무방향 그래프 G에 있는 모든 정점쌍에 대하여 항상 경로가 존재한다면 G는 연결되었다고 하며 이러한 무방향 그래프 G를 연결 그래프(connected graph)라 부릅니다. 그렇지 않은 그래프는 비연결 그래프(unconnected graph)라고 합니다. 트리는 그래프의 특수한 형태로서 사이클을 가지지 않는 연결 그래프입니다.

완전 그래프

그래프에 속해 있는 모든 정점이 서로 연결되어 있는 그래프를 완전 그래프(complete graph)라고 합니다. 무방향 완전 그래프의 정점 수를 n이라고 하면 하나의 점점은 n-1개의 다른 정점으로 연결 되므로 간선의 수는 n(n-1)/2가 됩니다.