[백준] 10775번: 공항

이미지를 클릭하면 문제로 이동합니다.

저는 처음에 이 문제를 indexed tree를 이용해서 풀었습니다. 그런데 백준의 알고리즘 분류를 보니 disjoint set이더군요! 그래서 disjoint set을 이용해서 다시 풀어보았습니다. 문제를 푸는 방법은 여러개가 있으니까요! 그래서 오늘은 먼저 disjoint set으로 문제를 푸는 방법을 설명해드리도록 하겠습니다. indexed tree를 이용해서 문제를 푸는 방법은 다음에 기회가 된다면 소개해 드리도록 하겠습니다.

문제 분석

1. $i$번쨰 비행기는 1번부터 $g_i$ 번째 게이트 중 하나에 영구적으로 도킹할 수 있습니다
   • $g_i$ 보다 같거나 작은 수에만 도킹할 수 있으므로 최대한 큰 수에 저장하는 것이 유리하겠군요
     • 왜냐하면 더 작은 수에는 도킹이 가능하지만 더 큰 수에는 도킹이 불가능하기 때문입니다
     • 예를들어 $g_1 = 2$이고 $g_2 = 1$인데 $g_1$을 1에 도킹시켰다면 $g_2$는 도킹할 수 없지만 $g_1$을 2에 도킹시키면 $g_2$도 1에 도킹시킬 수 있습니다
   • 일단 비행기가 $i$ 번째 비행기는 $g_i$가 비어있으면 $g_i$에 도킹하고 비어있지 않다면 한 칸 앞에, 한 칸 앞도 비어있지 않다면 한 칸 더 앞에 … 이런식으로 비어있는 공간을 찾을때까지 탐색하면 되겠군요
     • 더 이상 앞에 공간이 없다면 탐색을 종료하면 되겠군요
     • 포인터처럼 지금 자리에서 몇 번째 앞에 빈 공간이 있는지 알려주면 좋겠네요
   • 도킹하지 못하면 공항 운영이 종료됩니다

문제 풀이

예제 2를 가지고 문제를 풀어보도록 하겠습니다.

공항에는 4개의 게이트가 있고 6대의 비행기가 차례로 들어오게 됩니다

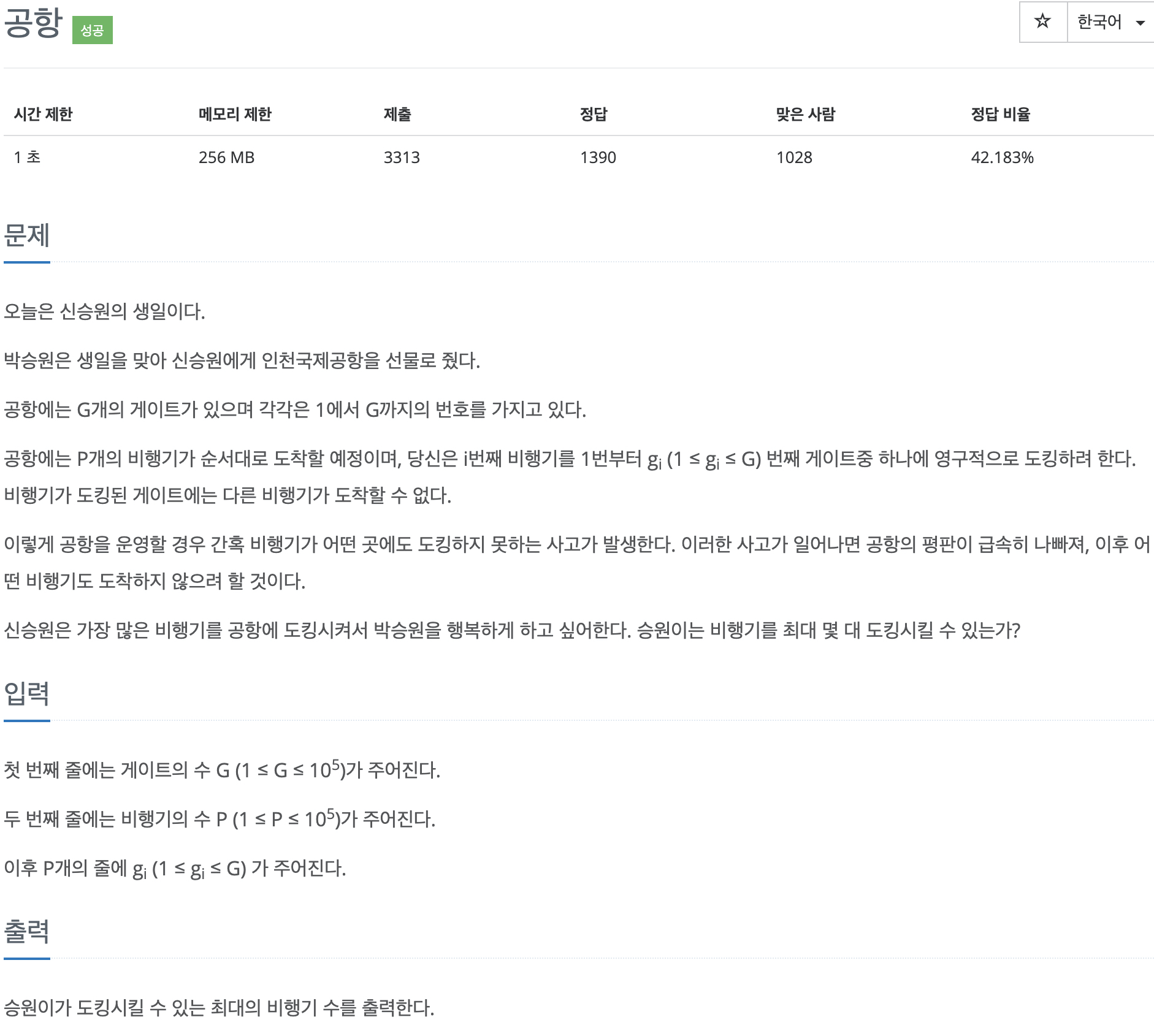
처음에는 모든 게이트가 비어있으니 각 게이트가 자기 자신을 가르키고 있게 세팅해줍니다.

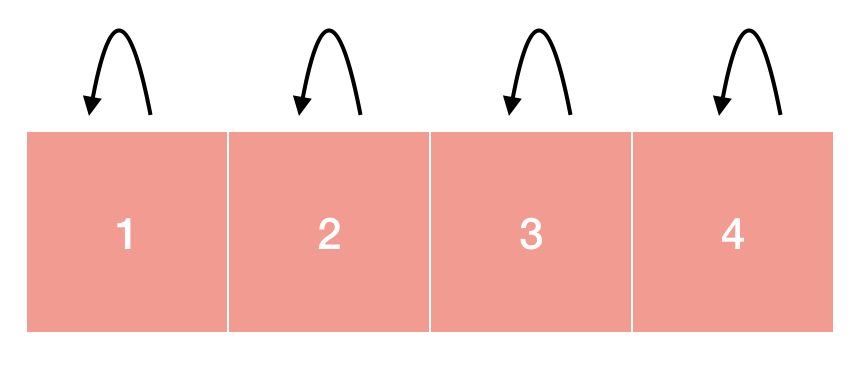
게이트 2에 비행기 한 대가 들어오고 게이트 2에는 더 이상 비행기를 도킹할 수 없게 되었습니다. 따라서 게이트 2에 들어오는 비행기는 게이트 1에 도킹할 수 있도록 해줍니다.

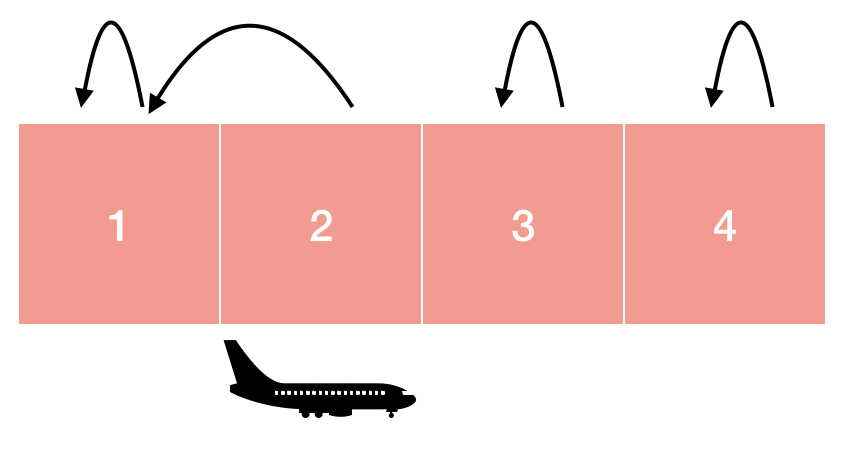
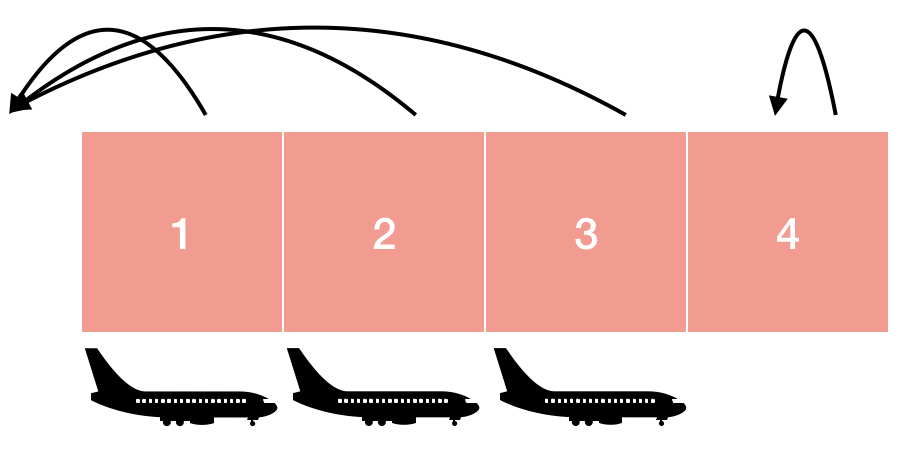
게이트 2에 비행기가 한 대 더 들어오고 그 비행기는 화살표를 따라서 게이트 1에 도킹하게 됩니다. 게이트 1 앞에는 더이상 게이트가 없으므로 게이트 2나 게이트 1에 비행기가 들어오게 되면 더이상 어떤 비행기도 도킹할 수 없게 됩니다.

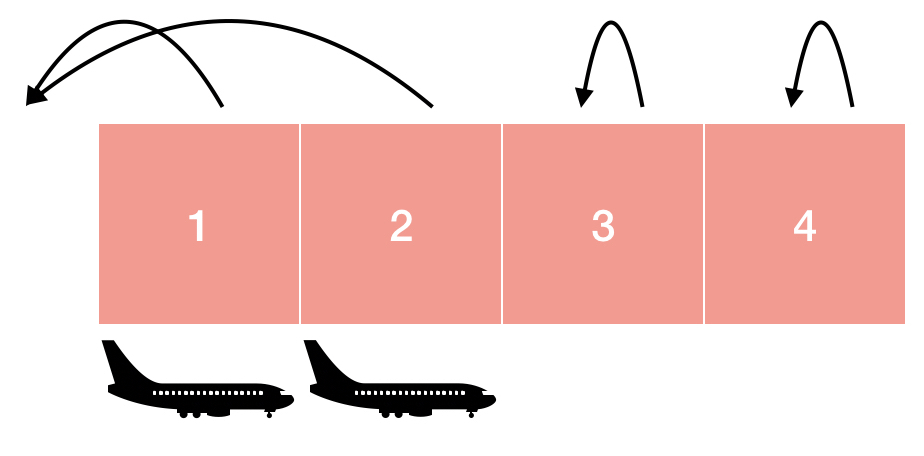
게이트 3에 비행기가 한 대 더 들어오고 게이트 3에 도킹하게 됩니다. 게이트 3에 비행기가 들어오면 게이트 2에 도킹을 해야하는데 게이트 2와 게이트 1이 모두 꽉 차있으므로 게이트 3에 비행기가 들어오게 되면 더이상 비행기를 도킹할 수 없게 됩니다.

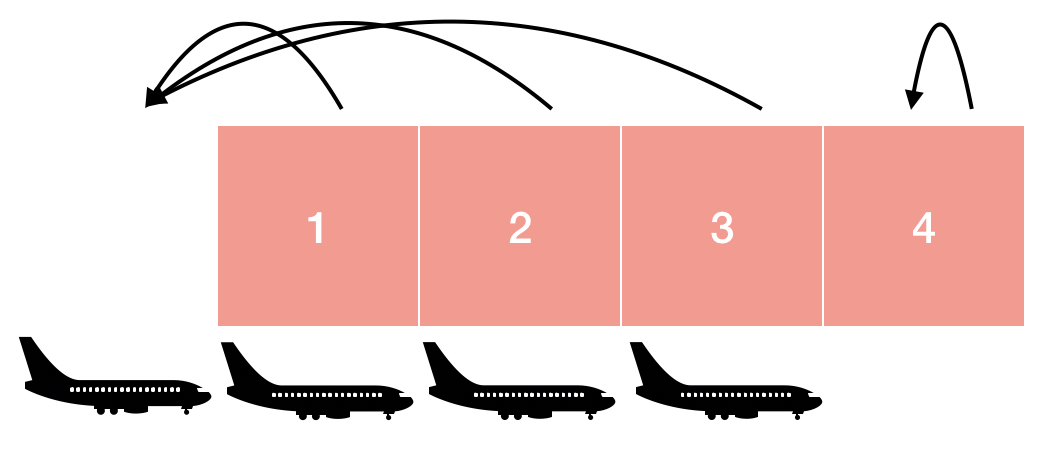
게이트 3에 비행기가 한 대 더 들어옴으로서 함수는 끝나게 됩니다.

이렇게 서로 다른 집단 두개를 합쳐주는 알고리즘을 Union-Find라고 합니다. 여기서 화살표가 가르키고 있는 대상을 부모라고 생각하고 같은 부모를 같고 있는 집단은 같은 집단에 속해있다고 생각하면 됩니다. 부모노드는 화살표기 자기 자신을 가르키는 노드를 찾을때까지 재귀적으로 타고 들어가서 찾을 수 있습니다.

Code

#include <stdio.h>
#define MAX 100010

int G, P, plane[MAX], airport[MAX], cnt = 0;

void input(){
    scanf("%d %d", &G, &P);
    for (int i = 0; i < P; i++){
        scanf("%d", &plane[i]);
    }
}

// 초기화. 모든 노드가 자기 자신을 가르키고 있게 해줌
void init(){
    for (int i = 1; i <= G; i++){
        airport[i] = i;
    }
}

// 자기 자신을 가르키는 노드가 나올때까지 재귀적으로 찾음
int Find(int a){
    if (airport[a] == a) return a;
    return airport[a] = Find(airport[a]);
}

// 부모가 같게 하여 서로 다른 두 집단을 합쳐줌
void Union(int a, int b){
    int parentA = Find(a);
    int parentB = Find(b);
    airport[parentA] = parentB;
}

void solve(){
    input();
    init();
    for (int i = 0; i < P; i++){
        int parentI = Find(plane[i]);
        // 더이상 게이트가 없으면 함수 종료
        if (parentI == 0) {
            break;
        }
        Union(parentI, parentI-1);
        cnt++;
    }
    printf("%d\n", cnt);
}

int main(void){
    solve();
    return 0;
}