[Algorithm] 기하 기초

기하학의 정의는 위키피디아를 참고하였습니다.

기하학의 정의

기하학은 공간에 있는 도형의 성질 즉, 대상들의 치수, 모양, 상대적 위치 등을 연구하는 수학은 한 분야입니다.

기초 기하

기하학이 다루는 대상으로는 점, 선, 면, 도형, 공간과 같은 것이 있습니다.

벡터와 스칼라

• 스칼라: 크기만 있고 방향을 가지지 않는 물리량
• 벡터: 크기와 방향을 가지는 물리량

벡터 연산

• 벡터의 합: 벡터의 각 성분끼리의 합
• 벡터의 차: 벡터의 각 성분끼리의 차

벡터의 곱

내적

• 정의: \(\vec{a} = (x_a, y_a)\), \(\vec{b} = (x_b, y_b)\)이고 $\vec{a}$와 $\vec{b}$가 이루는 각을 $\theta$라고 할 때, $\vec{a}$와 $\vec{b}$의 내적은 두 백터의 스칼라 곱인 \(\vec{a} \cdot \vec{b} = \begin{cases} x_ax_b + y_ay_b \\ |\vec{a}||\vec{b}|cos\theta \end{cases}\) 입니다
• 내적의 결과는 스칼라량입니다

외적

• 정의: \(\vec{a} = (x_a, y_a)\), \(\vec{b} = (x_b, y_b)\)이고 $\vec{a}$와 $\vec{b}$가 이루는 각을 $\theta$라고 할 때, $\vec{a}$와 $\vec{b}$의 외적은 두 벡터의 벡터 곱인 \(\vec{a} \times \vec{b} = \vec{n}( |\vec{a}||\vec{b}|\sin(\theta) )\) 입니다. ( $\vec{n}$은 $\vec{a}$와 $\vec{b}$에 모두 수직인 단위 벡터이고 $|\vec{a}||\vec{b}|\sin(\theta)$는 $\vec{a}$와 $\vec{b}$의 외적의 크기입니다. )
• 외적의 결과는 벡터입니다

기하 알고리즘 문제

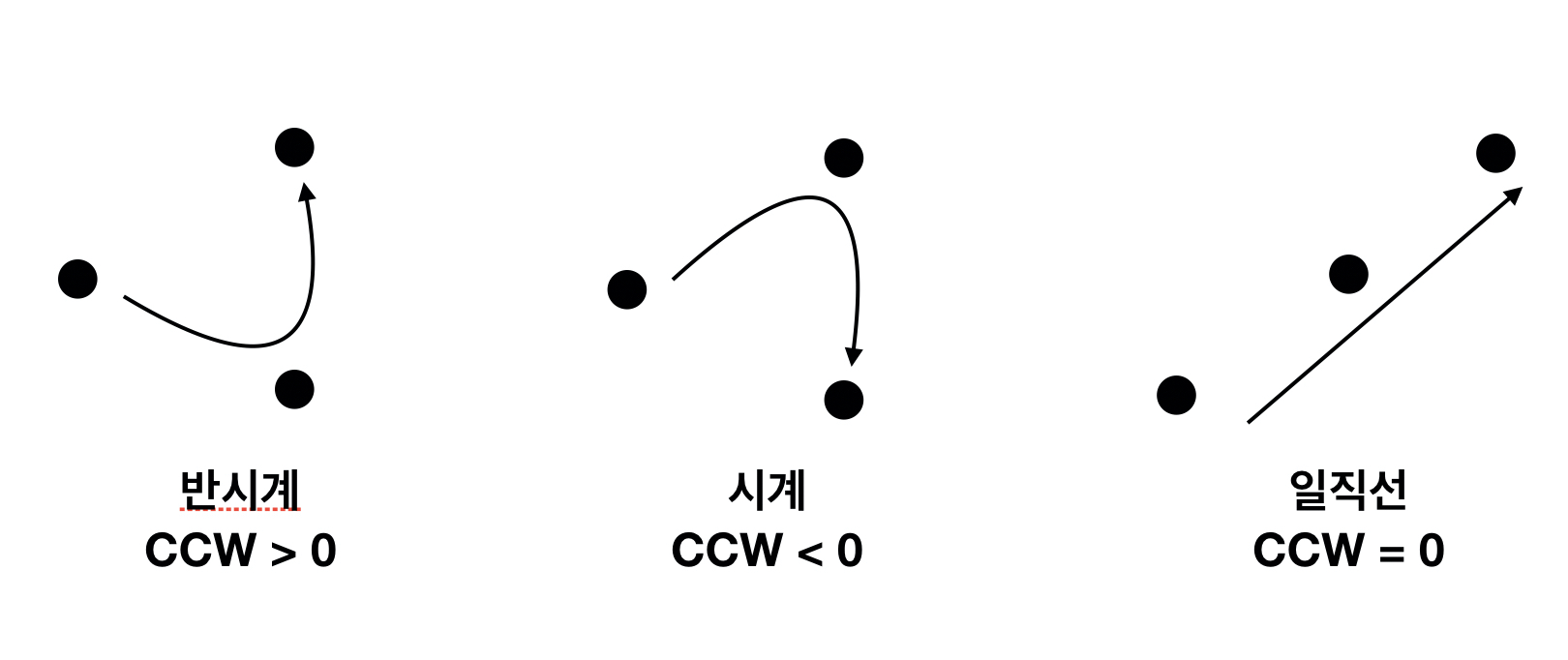
CCW

알고리즘에서 사용 되는 대표적인 기하학적 성질은 CCW가 있습니다. CCW란 counter clock wise의 약자로 벡터의 외적을 이용하여 평면상에 세 점이 있을 때 점들의 위치관계를 판단할 수 있는 알고리즘입니다. 기하 알고리즘은 모두 CCW를 이용해서 풀 수 있다고 해도 과언이 아닐 정도로 자주 쓰입니다. CCW식은 다음과 같습니다.

$$|\vec{a} \times \vec{b}| = |\vec{a}| |\vec{b}| \sin\theta$$ \[\begin{align*} CCW(ax, ay, bx, by, cx, cy) &= (ax \times by + bx \times cy + cx \times ay) \\ & - (ay \times bx + by \times cx + cy \times ax) \end{align*}\]

세 점의 회전방향이 반시계인 경우 CCW값은 +, 시계 방향인 경우 CCW값은 -, 세 점이 일직선 상에 있는 경우 CCW값은 0이 나옵니다. 여기서 CCW의 값보다는 부호가 중요합니다.

문제 예시

• 모든 점들을 포함하는 폐쇠경로 찾기
  • 임의의 기준점 설정 후 비교 함수로 ccw의 부호를 사용한 각도정렬
• 선분 교차 여부 찾기
  • 선분 \(\overline{AB}\)와 선분 \(\overline{CD}\)가 교차하는지 알기 위해 CCW를 활용할 수 있습니다
  • \(CCW(A, B, C) \times CCW(A, B, D) < 0\) 이고 \(CCW(C, D, A) \times CCW(C, D, B) < 0\) 이면 두 선분은 교차한다
  • 두 선분이 맞닿는 경우에 대한 예외처리가 필요할 수 있다
• 점의 다각형 포함 판별 여부 찾기
  • 점 P가 N개의 점으로 이루어진 다각형내에 포함되는지 찾기위해 CCW를 사용할 수 있습니다
• 볼록껍질 접근법
  • N개의 주어진 점들 중 모든 임의의 두 점을 연결하는 선분이 항상 다각형 내부에 존재하도록 하는 점들을 찾는 문제
  • 해당 문제에 대한 보단 자세한 풀이법은 “[백준] 1708번: 볼록 껍질”을 확인하시길 바랍니다