[백준] 1948번: 임계경로

이미지를 클릭하면 문제로 이동합니다.

출발 도시는 들어오는 도로가 0개이고 도착 도시는 나가는 도로가 0개라는 문구에서 위상정렬 문제라는 힌트를 얻을 수 있습니다. 이 문제는 두 개의 문제로 나눌 수 있습니다.

1. 도착 지점까지 가는 가장 오래 걸리는 시간
2. 도착 지점까지 가장 오래 걸리게 가는 루트에 포함된 도로의 갯수

1. 도착 지점까지 가는 가장 오래 걸리는 시간

첫 번째 파트는 기존 위상정렬 문제를 푸는 방식으로 접근할 수있습니다. 기존 위상정렬 문제와의 차이점은 시작지점으로 부터 해당 도시까지 가는 가장 오래 걸리는 시간을 따로 기록해주어야 한다는 것입니다. 도시 A로부터 도시 B까지 가는데 t시간 만큼 걸린다고 할 때 시작점으로 부터 도시 B 까지 가는데 가장 오래 걸리는 시간은 다음 식으로 업데이트 할 수 있습니다.

\[time(B) = \max(time(B), time(A) + t)\]

2. 도착 지점까지 가장 오래 걸리게 가는 루트에 포함된 도로의 갯수

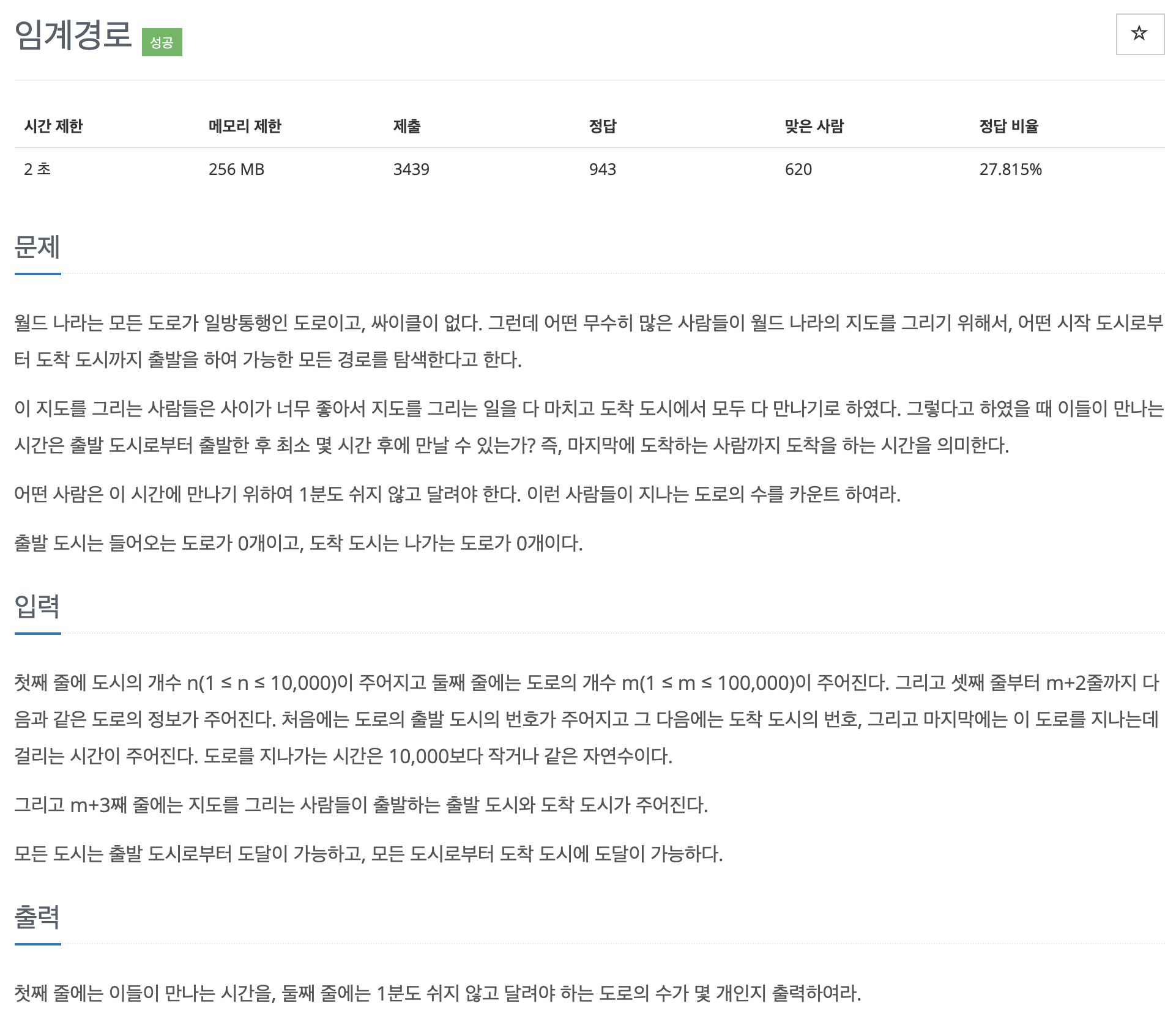
두 번째 파트는 조금 주의해야합니다. 먼저 도착지점까지 가는 가장 오래 걸리는 루트는 하나가 아닐 수 있습니다. 문제에 있는 예시로 한번 살펴보도록 하겠습니다.

이 예제에서 시작지점인 1에서 도착지점인 7까지 가장 오래 걸리는 시간은 12초이고 1에서 7까지 가는데 12초가 걸리는 루트 총 2가지가 있습니다.

여기서 주의해야할 점은 중복되는 루트는 한 번만 세어 주어야 한다는 것입니다.

두 번째 파트를 풀기 위해서는 도착지점에서 부터 시작지점까지 되돌아가며 구할 수 있습니다. 첫 번째 파트 풀면서 시작지점으로 부터 해당 도시 까지 가는 데 가장 오래 걸리는 시간을 기록해 두었기 때문에 이것을 활용하여 두 번째 파트를 풀 수 있습니다. 시작점으로 부터 도시 A까지 가는 가장 오래 걸리는 루트가 a초 걸리고 시작점으로 부터 도시 B까지 가는 가장 오래 걸리는 루트가 b초 걸린다고 했을 때 $(a < b)$ 도시 A로부터 도시 B까지 가는데 $b - a$초 만큼 걸린다면 그 도로는 가장 오래 걸리는 루트에 포함됩니다.

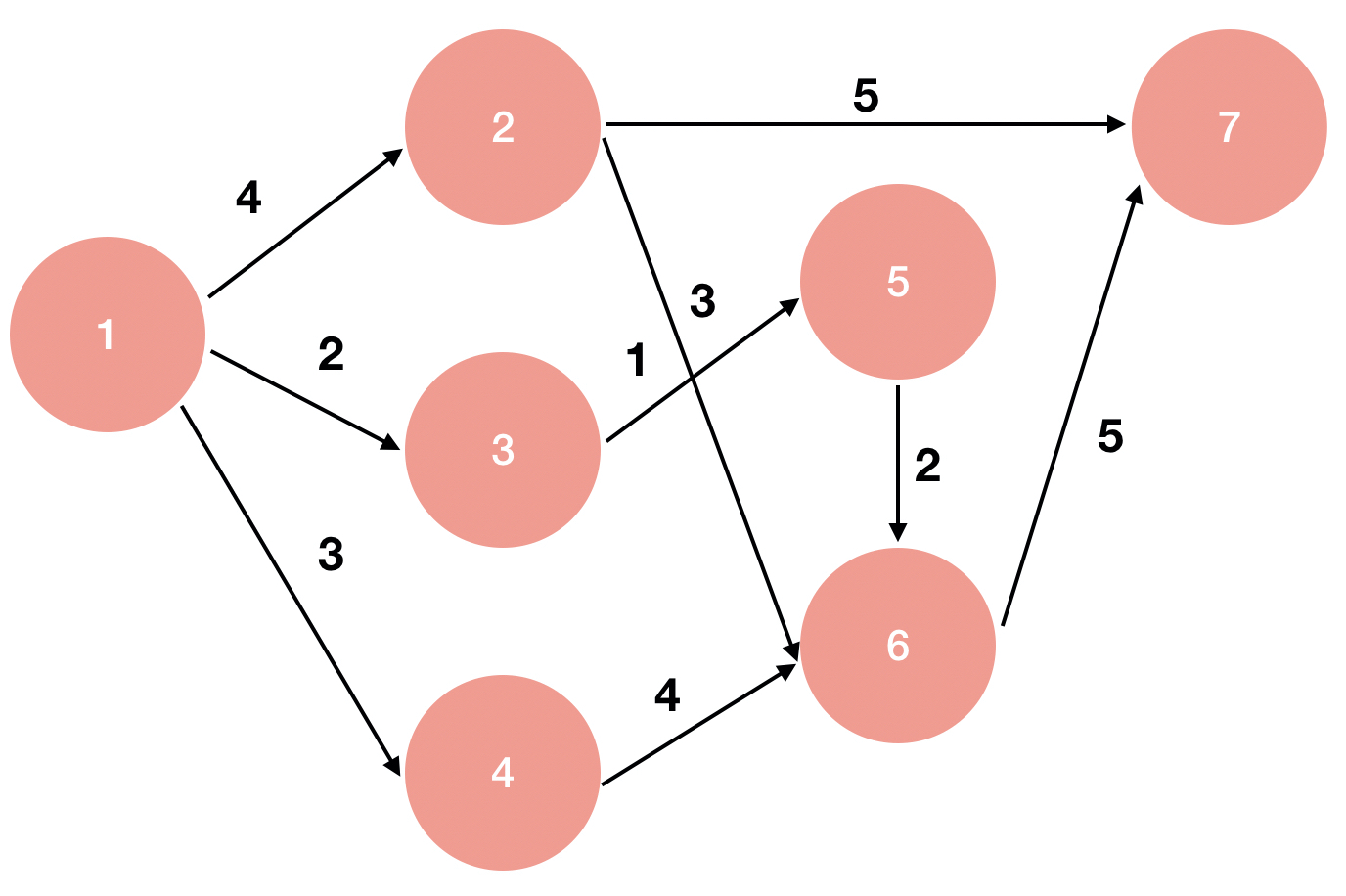
위의 그림으로 예시를 들어 본다면 도시 1에서 도시 7까지 가는데 가장 오래 걸리는 시간은 12입니다. 도시 1에서 도시 6까지 가는데 가장 오래 걸리는 시간은 7초 입니다. 도시 6에서 도시7까지 가는데 5초가 걸리므로 도시 6에서 도시7까지 가는 도로는 가장 오래 걸리는 루트에 포함되게 됩니다. 하지만 도시 1에서 도시 2까지 가는데 걸리는 가장 도래 걸리는 시간은 4초이고 $4 + 5 \neq 12$이기 때문에 도시 2에서 도시 7까지 가는 도로는 가장 오래 걸리는 루트에 포함될 수 없습니다.

Code

#include <stdio.h>
#include <queue>
#include <vector>
#define MAX 10010

using namespace std;

typedef struct {
    int x, t;
} road;

int N, M, numRoad = 0, START, END, maxTime;
int inRoad[MAX], TIME[MAX] = {0, }, checkCity[MAX] = {0, };

vector <road> fromto[10010], tofrom[10010];
// fromto: 출발 도시로부터 갈 수 있는 도착 도시와 걸리는 시간을 저장한 벡터. maxTime을 찾는데 사용
// tofrom: 도착 도시로부터 갈 수 있는 출발 도시와 걸리는 시간을 저장한 벡터. numRoad를 찾는데 사용

queue <int> city, roadTime;
// city: maxTime을 찾기 위해 시작점으로 부터 위상정렬을 할 때 사용되는 queue
// roadTime: numRoad를 찾기 위해 도착점으로 부터 위상을 할 때 사용되는 queue

road makeRoad(int x, int t){
    road tmp;
    tmp.x = x, tmp.t = t;
    return tmp;
}

void input(){
    scanf("%d", &N);
    scanf("%d", &M);
    int x, y, t;
    for (int i = 0; i < M; i++){
        scanf("%d %d %d", &x, &y, &t);
        fromto[x].push_back(makeRoad(y, t)); 
        inRoad[y] ++;
        tofrom[y].push_back(makeRoad(x ,t));
    }
    scanf("%d %d", &START, &END);
}

// maxTime을 찾기 위해 시작점으로 부터 위상정렬을 하는 함수
void topologicalSort(){
    city.push(START);
    while(!city.empty()){
        int curCity = city.front();
        city.pop();
        for (int i = 0; i < fromto[curCity].size(); i++){
            int nextCity = fromto[curCity][i].x;
            int nextTime = fromto[curCity][i].t;
            if (TIME[nextCity] < TIME[curCity] + nextTime){
                TIME[nextCity] = TIME[curCity] + nextTime;
            }
            inRoad[nextCity] --;
            // 해당 도시로 들어오는 길이 없을 때만 queue에 넣어준다
            if (inRoad[nextCity] == 0){
                city.push(nextCity);
            }
        }
    }
}

// numRoad를 찾기 위해 도착점으로 부터 거꾸로 위상정렬을 하는 함수
void findRoad(){
    roadTime.push(END);
    while(!roadTime.empty()){
        int curCity = roadTime.front();
        roadTime.pop();
        for (int i = 0; i < tofrom[curCity].size(); i++){
            int prevCity = tofrom[curCity][i].x;
            int prevTime = tofrom[curCity][i].t;
            if (TIME[curCity] - prevTime == TIME[prevCity]){
                numRoad++;
                // 최장 시간 루트에 포함 되는 도시이고 아직 방문을 안한 도시일때만 queue에 넣어주어서 중복으로 방문하는 것 방지
                if (checkCity[prevCity] == 0){
                    roadTime.push(prevCity);
                    checkCity[prevCity] = 1;
                }
            }
        }
    }
}

void solve(){
    input();
    topologicalSort();
    findRoad();
    printf("%d\n%d", TIME[END], numRoad);
}

int main(void){
    solve();
}