[백준] 13460번: 구슬 탈출 2

이미지를 클릭하면 문제로 이동합니다.

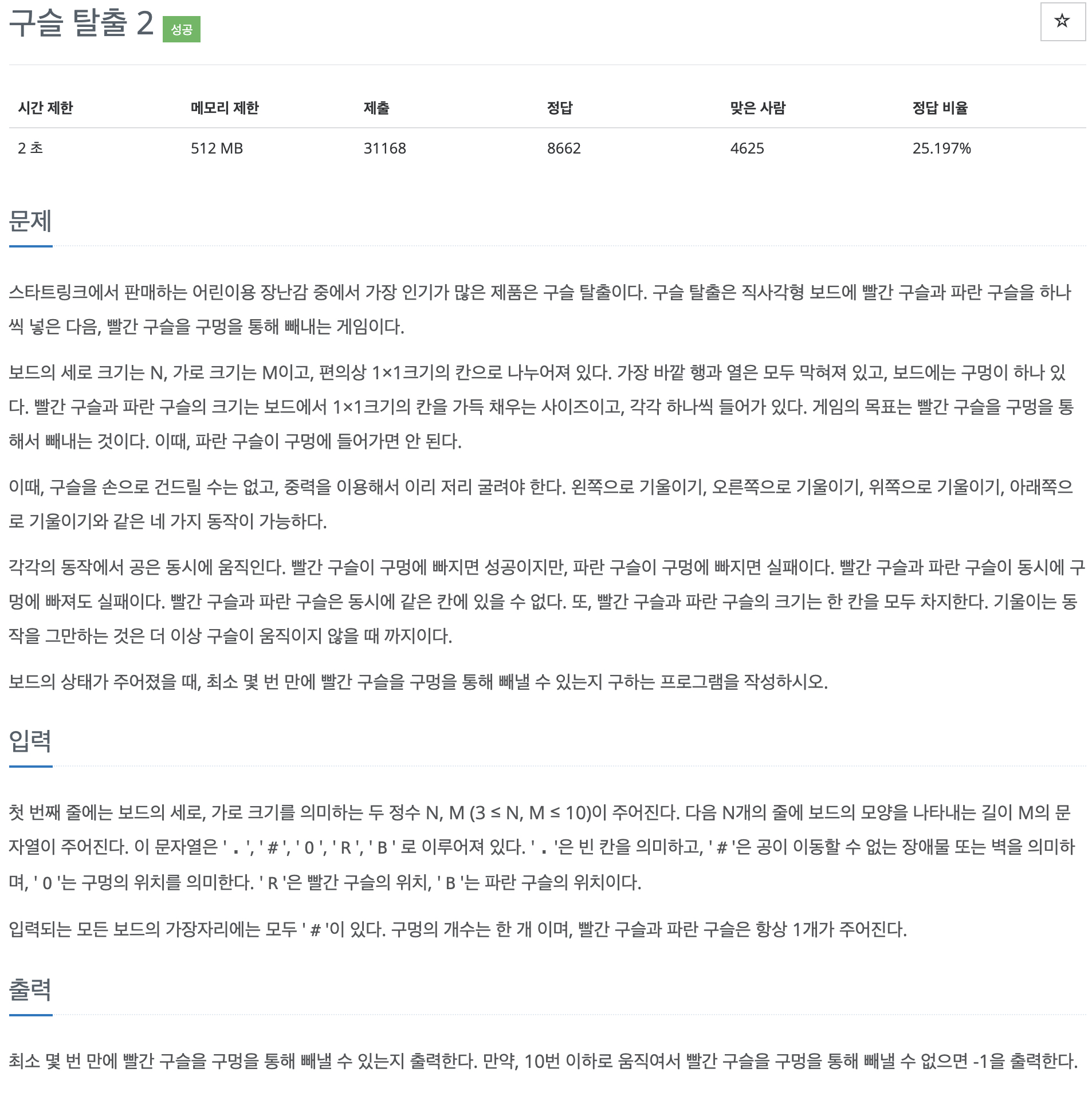
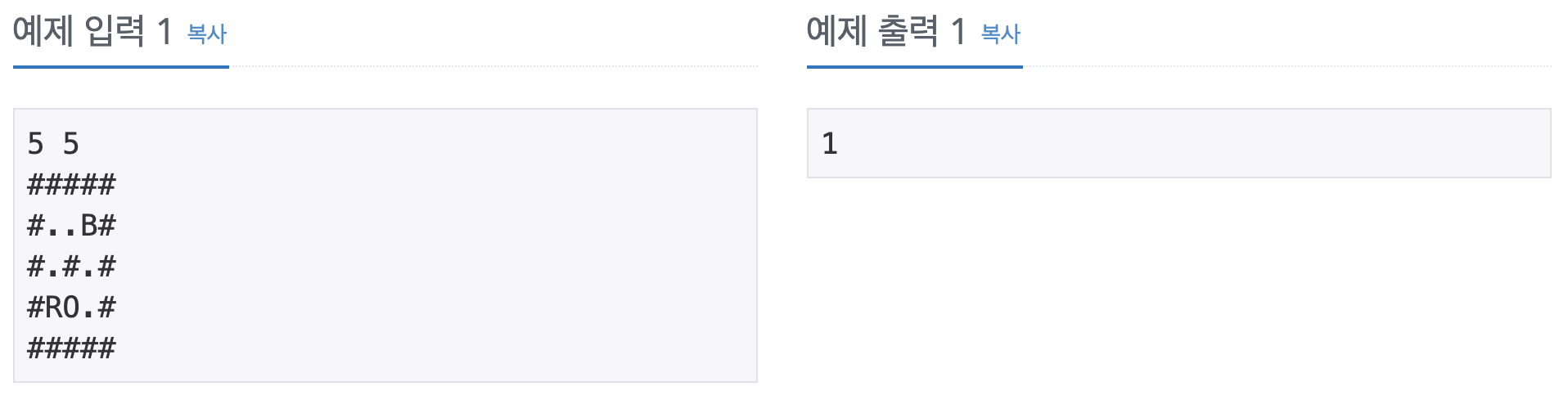
문제 분석을 시작하기 앞서 먼저 예제 입력을 살펴보도록 하겠습니다.

굉장히 미로같이 생겼습니다. 또한 문제에서 미로의 가로 세로 크기의 범위가 $3 \leq N, M \leq 10$인것과 구슬이 10번 이하로 움직인다는 것에서 모든 가능한 경우를 다 탐색해야하는 완전 탐색 (Brute Force) 문제인 것을 눈치챌 수 있습니다. 완전 탐색 문제는 시간복잡도가 높기 때문에 입력의 범위가 크다면 시간초과에 걸리는 경우가 많아서 입력의 범위가 작으면 ‘완전탐색 문제인가?’ 하고 의심해 볼 수 있습니다.

다만 이 문제는 일반적인 완전탐색 문제에서 추가되는 조건이 좀 있기 때문에 한번 더 생각해야 합니다. 완전탐색을 하는 알고리즘에는 대표적으로 BFS와 DFS가 있습니다. 그렇다면 여기서는 BFS와 DFS중 어느 것을 사용해야 할까요?

BFS와 DFS 둘 다 사용 가능한 경우도 있지만 이 경우에서는 BFS가 조금 더 적합합니다. DFS의 경우에는 하나의 루트가 도착점까지 도달할 수 있는가?에대한 문제를 푸는 것이기 때문에 도착점에 도달하는 가장 빠른 루트를 찾는데는 BFS가 조금 더 적합하다고 할 수 있습니다. 물론 DFS가 불가능하다는 것은 아니지만 이번 포스팅에선 BFS로 접근해보도록 하겠습니다.

1. BFS 탐색 규칙

BFS로 문제를 접근한다면 탐색할 때 어떤 순서로, 또 어떤 규칙에 따라 탐색을 해야하는지 문제 분석을 통해 정해보도록 하겠습니다

1. 빨간공과 파란공은 함께 움직입니다
   • 두 공의 좌표를 함께 queue에 저장해 주는 것이 좋을 것 같음
   • 구조체를 정의하는게 편하겠군요
2. 방향이 바뀔때만 count를 늘려줍니다
   • 이전 방향이 어딘지 알고있어야 하겠군요
   • 이전 방향과 같은 방향으로 가는건 의미가 없습니다
     • 이전 방향에서 이미 해당방향으로 갈 수 있는 끝까지 갔기때문에 같은 방향으로 또 가는건 의미가 없습니다
     • 꼭 필요하진 않지만 시간을 줄일 수는 있겠군요
3. 빨간공과 파란공은 같은 자리에 있을 수 없습니다
   • 이동을 더 많이 한 공이 뒤에 있었겠군요
     • 공이 몇칸을 이동했는지 세어주면 편할 것 같습니다

2. 게임 규칙

BFS탐색 규칙을 정했다면 게임 진행 방식과 이기는 규칙도 분석을 해보도록 하겠습니다

1. 공은 벽을 마주칠때까지 움직입니다
2. 게임이 끝나는 시나리오는 3가지가 있습니다
   1. 빨간공과 파란공이 동시에 구멍에 들어감
      • 이 경우 게임이 지게 됩니다
        • 이 경우에서는 다른 루트로 게임을 이길 수 있나 탐색을 진행하게 됩니다
   2. 파란색 공만 구멍에 들어감
      • 이 경우에도 게임이 지게 됩니다
        • 마찬가지로 다른 루트 탐색을 진행합니다
   3. 빨간색 공만 구멍에 들어감
      • 이 경우에는 게임이 이기게 되고 BFS의 특성상 가장 먼저 찾은 루트가 최소 시간 루트이므로 바로 탐색을 종료할 수 있습니다

Code

#include <stdio.h>
#include <queue>

using namespace std;

#define MAX 20
const int dir[4][2] = { {-1,0}, {1,0}, {0,-1}, {0,1} }; // 상 하 좌 우
int N, M, map[MAX][MAX], RX, RY, BX, BY, ans = -1;

struct Node {
    int rx, ry, bx, by, d, cnt;
};
// 빨간공과 파란공의 좌표, 이전 방향, 방향을 바꾼 횟수를 저장
Node makeNode(int rx, int ry, int bx, int by, int d, int cnt){
    Node tmp;
    tmp.rx = rx, tmp.ry = ry, tmp.bx = bx, tmp.by = by, tmp.d = d, tmp.cnt = cnt;
    return tmp;
}


void input(){
    scanf("%d %d", &N, &M);
    for (int i = 0; i < N; i++){
        char tmp[MAX];
        scanf("%s", tmp);
        for (int j = 0; j < M; j++){
            map[i][j] = tmp[j];
            if (map[i][j] == 'R'){
                RX = i, RY = j;
            }
            else if (map[i][j] == 'B'){
                BX = i, BY = j;
            }
        }
    }
}

void bfs() {
    queue <Node> q;
    q.push(makeNode(RX, RY, BX, BY, -1, 0));
    while (!q.empty()){
        int rx, ry, bx, by, d, cnt;
        rx = q.front().rx, ry = q.front().ry;
        bx = q.front().bx, by = q.front().by;
        d = q.front().d, cnt = q.front().cnt;
        q.pop();
        for (int i = 0; i < 4; i++){
            // 이전에 방향을 바꾼 방향과 같거나 10번 이상 방향을 바꿨으면 다음으로 넘어감
            if (i == d || cnt >= 10) continue;

            int rnx, rny, bnx, bny, redMove=0, blueMove=0;
            bool redIn = false, blueIn = false;

            // 빨간공 먼저 이동
            rnx = rx;
            rny = ry;
            // 벽을 만날 때까지 움직임
            while (map[rnx][rny] != '#'){
                rnx += dir[i][0];
                rny += dir[i][1];
                redMove ++;
                // 빨간공이 구멍에 들어감
                if (map[rnx][rny] == 'O'){
                    redIn = true;
                    break;
                }
            }
            rnx -= dir[i][0];
            rny -= dir[i][1];

            // 파란공 이동
            bnx = bx;
            bny = by;
            // 벽을 만날 때까지 움직임
            while (map[bnx][bny] != '#'){
                bnx += dir[i][0];
                bny += dir[i][1];
                blueMove++;
                // 파란공이 구멍에 들어감
                if (map[bnx][bny] == 'O'){
                    blueIn = true;
                    break;
                }
            }
            bnx -= dir[i][0];
            bny -= dir[i][1];

            // 이동 후 두 공의 좌표가 같다면 더 많이 움직인 공을 한 칸 뒤로 옮김
            if (rnx == bnx && rny == bny){
                if (redMove < blueMove){
                    bnx -= dir[i][0];
                    bny -= dir[i][1];
                }
                else {
                    rnx -= dir[i][0];
                    rny -= dir[i][1];
                }
            }

            // 게임이 끝나는 시나리오 3.
            if (redIn && !blueIn){
                ans = cnt+1;
                return;
            }
            // 아예 이동하지 않았으면 다시 queue에 넣어주지 않는다
            else if (rnx == rx && rny == ry && bnx == bx && bny == by){
                continue;
            }
            // 파란공이 구멍에 들어가는 경우는 어떤 경우라도 더 탐색을 진행해봤자 게임이 끝나게 된다
            // 파란공이 구멍에 들어가지 않은 경우만 탐색 진행
            else if (!blueIn){
                q.push(makeNode(rnx, rny, bnx, bny, i, cnt+1));
            }



        }

    }
}


void solve(){
    input();
    bfs();
    printf("%d\n", ans);
}

int main(void){
    solve();
    return 0;
}